题目内容
如图，三角形是直角三角形，则三个半圆的面积的大小关系是（ ）分析：设三角形的三边分别为a、b、c，根据圆的面积表示出三个半圆的面积，再根据勾股定理得到a、b、c的关系，从而得解．
解答：
解：如图，设三角形的三边分别为a、b、c，
则S1=
×
πb2=
πb2，S2=
πa2，S3=
πc2，
∵三角形是直角三角形，
∴a2+b2=c2，
∴S1+S2=S3．
故选C．
解：如图，设三角形的三边分别为a、b、c，则S1=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
∵三角形是直角三角形，
∴a2+b2=c2，
∴S1+S2=S3．
故选C．
点评：本题考查了勾股定理，用直角三角形的三条边表示出三个半圆的面积是解题的关键．
练习册系列答案
相关题目
（1）如图，∠AOB是直角，OD平分∠BOC，OE平分∠AOC，求∠EOD的度数．
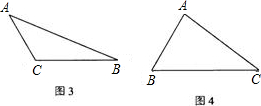
如图，三角形是直角三角形，则三个半圆的面积的大小关系是