题目内容
（1）欲求1+3+32+33+…+320的值，可令S=1+3+32+33+…+320…①，将①式两边同乘以3，得______…②，由②式减去①式，得S=______．
（2）仿照（1）的方法，当k≠1时，试求a+ak+ak2+ak3+…akn的值（用含a，n，k的代数式表示）
解：（1）3S=3+32+…+321…②，
②-①得：2S=321-1，即S=
（321-1）；
（2）设M=a+ak+ak2+ak3+…akn，①
两边都乘以k得：kM=ak+ak2+ak3+…akn+1，②
②-①得：（k-1）M=akn+1-a，即M=
，
则a+ak+ak2+ak3+…akn=．
故答案为：（1）3S=3+32+…+321；（321-1）
分析：（1）将已知的等式左右两边乘以3即可得到结果，两式相减即可求出S；
（2）将所求等式设为M，左右两边乘以k后，两式相减即可用a，n及k表示出结果．
点评：此题考查了整式的混合运算，解本题的关键是熟练运用错位相减法．
②-①得：2S=321-1，即S=
（321-1）；（2）设M=a+ak+ak2+ak3+…akn，①
两边都乘以k得：kM=ak+ak2+ak3+…akn+1，②
②-①得：（k-1）M=akn+1-a，即M=
，则a+ak+ak2+ak3+…akn=
．故答案为：（1）3S=3+32+…+321；
（321-1）分析：（1）将已知的等式左右两边乘以3即可得到结果，两式相减即可求出S；
（2）将所求等式设为M，左右两边乘以k后，两式相减即可用a，n及k表示出结果．
点评：此题考查了整式的混合运算，解本题的关键是熟练运用错位相减法．
练习册系列答案
计算高手系列答案
相关题目
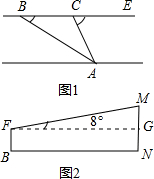米到C处，再观察A，此时视线CA与河岸所成的夹角∠ACE=64°．