题目内容
如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在 轴的正半轴上,OC=6, B(9,4)
轴的正半轴上,OC=6, B(9,4)
(1)求tan AOC
AOC
(2)D从C点出发,延CO方向以每秒0.75单位的速度运动,点E从O点出发以每秒2个单位的速度,沿线段OA, AB运动,当t为多少时,直线DE平分平行四边形OABC的面积。
(3)在(2)中的直线上是否存在一点P使 ⊿BEP 与⊿BEC相似,若存在求点P的坐标,若不存在请说明理由。
⊿BEP 与⊿BEC相似,若存在求点P的坐标,若不存在请说明理由。

解:(1)tan AOC=
AOC=
 (2)
(2) DE平分平行四边形OABC的面积 ,AO=5
DE平分平行四边形OABC的面积 ,AO=5
∴AE=CD,即

(3) E(6,4) C(6、0)
E(6,4) C(6、0)
∴EC‖ 轴,∴⊿BEC 为RT⊿BEC.
轴,∴⊿BEC 为RT⊿BEC.
当⊿BEP与⊿BEC相似时;
当 位于如图
位于如图 时,
时,
 =
= ,
,
则 ‖EC‖
‖EC‖ 轴。
轴。
∴tan AOC= tan
AOC= tan
 =
= EB=3 ∴
EB=3 ∴ =4
=4
∴ (9,8)
(9,8)
当P位于如图 时,
时,
 =
= ,作
,作 ,垂足为G。
,垂足为G。

 =
= tan
tan
 =
=
∴
∴ EG=
EG= ∴
∴  (
( ,
, )
)
综上所述P点坐标为 ( ,
, )或(9,8)
)或(9,8)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

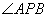 =90°
=90°
 的图象,使其与x轴交于两点,且此两点的距离为1个单位,则移动方式可为( )
的图象,使其与x轴交于两点,且此两点的距离为1个单位,则移动方式可为( )  (x>0),随着x值的增大,y值 .
(x>0),随着x值的增大,y值 .  的图象如图所示,反比例函数
的图象如图所示,反比例函数 与一次函数
与一次函数 在同一平面直角坐标系中的大致图象是( )
在同一平面直角坐标系中的大致图象是( )
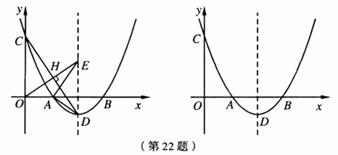
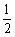 (x-3)2-1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D了.
(x-3)2-1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D了.