题目内容
5. 如图,在平面直角坐标系中,点C的坐标为(0,2),动点A以每秒1个单位长的速度从点O出发沿x轴的正方向运动,M是线段AC的中点,将线段AM以点A为中心,沿顺时针方向旋转90°得到线段AB.联结CB.设△ABC的面积为S,运动时间为t秒,则下列图象中,能表示S与t的函数关系的图象大致是( )
如图,在平面直角坐标系中,点C的坐标为(0,2),动点A以每秒1个单位长的速度从点O出发沿x轴的正方向运动,M是线段AC的中点,将线段AM以点A为中心,沿顺时针方向旋转90°得到线段AB.联结CB.设△ABC的面积为S,运动时间为t秒,则下列图象中,能表示S与t的函数关系的图象大致是( )| A. | 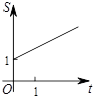 | B. | 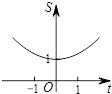 | C. | 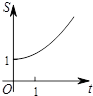 | D. | 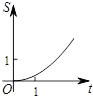 |
分析 用含t的代数式表示AC、AB,即可知S=$\frac{1}{2}$AC•AB,列出函数表达式,即可作出判断.
解答 解:∵点C的坐标为(0,2),
∴OC=2,
∵OA=t,
∴AC=$\sqrt{{t}^{2}+{2}^{2}}$=$\sqrt{{t}^{2}+4}$,
∵M是线段AC的中点,将线段AM以点A为中心,沿顺时针方向旋转90°得到线段AB.
∴AM=AB=$\frac{1}{2}$$\sqrt{{t}^{2}+4}$,
∴S=$\frac{1}{2}$AC•AB=$\frac{1}{4}{t}^{2}$+1.
∵t>0
∴函数的图象是C选项,
故选:C.
点评 本题主要考查了动点问题的图象,根据题意列出函数表达式是作出正确判断的关键.

练习册系列答案
相关题目
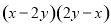 B.
B. 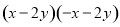
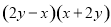 D.
D. 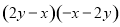
 是二次函数
是二次函数 的图象上两点,则
的图象上两点,则 ____
____ (填“>”、“<”或“=” )
(填“>”、“<”或“=” ) B.
B.  C.
C.  D.
D. 
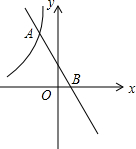 如图,一次函数y2=-2x+b(b为常数)的图象与反比例函数y1=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A,B两点,且点A的坐标为(-1,4).当y1<y2时,求x的取值范围.
如图,一次函数y2=-2x+b(b为常数)的图象与反比例函数y1=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A,B两点,且点A的坐标为(-1,4).当y1<y2时,求x的取值范围.