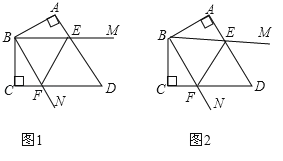
题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 分别从点
分别从点![]() 同时出发,点
同时出发,点![]() 以每秒1个单位的速度沿
以每秒1个单位的速度沿![]() 匀速运动.点
匀速运动.点![]() 沿折线
沿折线![]() 向终点
向终点![]() 匀速运动,在
匀速运动,在![]() 上的速度分别是每秒
上的速度分别是每秒![]() 个单位、每秒2个单位.当点
个单位、每秒2个单位.当点![]() 停止时,点
停止时,点![]() 也随之停止运动.连按
也随之停止运动.连按![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连按
,连按![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长.
的长.
(2)当点![]() 与
与![]() 的顶点重合时,求
的顶点重合时,求![]() 的长.
的长.
(3)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)点![]() 出发后,当
出发后,当![]() 与
与![]() 的边所夹的角被
的边所夹的角被![]() 平分时,直按写出
平分时,直按写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或1;(3)当
或1;(3)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(4)
;(4)![]() 或
或![]() 或
或![]()
【解析】
(1)由直角三角形的性质得出AB=2AC=2,BC=ACtan60°=![]() ,求出0<t≤
,求出0<t≤![]() ,得出PB=AB-AP=2-t(0<t≤
,得出PB=AB-AP=2-t(0<t≤![]() );
);
(2)由旋转的性质得出△PQD是等边三角形,①当点D与点C重合时,由等边三角形的性质得出∠PCQ=60°,得出∠ACP=90°-∠PCQ=30°,求出∠APC=90°,由三角函数即可得出答案; ②当点D与点A重合时,由等边三角形的性质得出此时点Q与点C重合,得出PQ=AC=1即可;
(3)分情况讨论①当![]() 时,过点Q作QH⊥AB于H,则
时,过点Q作QH⊥AB于H,则![]() 求出
求出![]() 得出
得出![]() 由勾股定理得出
由勾股定理得出![]() 即可得出答案;
即可得出答案;
②当![]() 时,过点Q作QH⊥AB于H,则
时,过点Q作QH⊥AB于H,则![]()
![]() 得出
得出![]() 由勾股定理得出
由勾股定理得出![]() 即可得出答案;
即可得出答案;
(4)①当PQ平分∠DPB时;②当PQ平分∠DQB时;③当PQ平分DQC时;求出t的值即可.
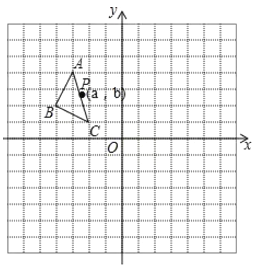
解:(1)∵Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=30°,
∴AB=2AC=2,BC=ACtan60°=![]() ,
,
∵点P以每秒1个单位的速度沿A→B匀速运动,
∴点P到点B用的时间为:![]() =2(秒),
=2(秒),
∵点Q沿折线BC→CA向终点A匀速运动,
在BC、CA上的速度分别是每秒![]() 个单位,每秒2个单位,
个单位,每秒2个单位,
∴点Q与点C重合时,用的时间为:![]() =1(秒),
=1(秒),
点Q从点C运动到点A用的时间为:![]() (秒),
(秒),
∵当点Q停止时,点P也随之停止运动,
∴0<t≤![]() ,
,
∴PB=AB-AP=2-t(0<t≤![]() );
);
(2))∵将PQ绕着点P逆时针旋转60°了得到PD,
∴△PQD是等边三角形, 分情况讨论:
①当点![]() 与点
与点![]() 重合时
重合时
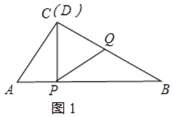
∵△PQD是等边三角形, ∴∠PCQ=60°,
∴∠ACP=90°-∠PCQ=90°-60°=30°,
∵∠A=60°,
∴∠APC=180°-∠A-∠ACP=180°-60°-30°=90°,
∴PQ=PC=ACsin60°=![]()
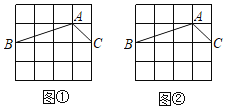
②当点D与点A重合时,如图2所示:
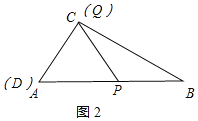
∵△PQD是等边三角形,∠A=60°,
∴此时点Q与点C重合,
∴PQ=AC=1;
综上所述,当点D与△ABC的顶点重合时,PQ的长为![]() 或1;
或1;
(3)分情况讨论:
①当![]() 时,过点Q作QH⊥AB于H,如图3所示:
时,过点Q作QH⊥AB于H,如图3所示:
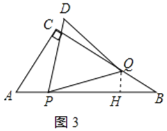
则QH=![]() BQ=
BQ=![]()
BH=BQcos30°=![]()
PH=PB-BH=![]()
![]()
![]()
![]()
②当![]() 时,
时,
过点Q作QH⊥AB于H,如图4所示:
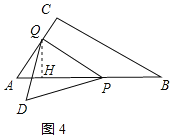
则AQ=![]()
![]()
QH=AQsin60°=![]()
∴PH=AP-AH=![]()
∴![]()
∴![]()
![]()
(4))①当PQ平分∠DPB时,如图5所示: 则∠QPB=∠DPQ=60°,
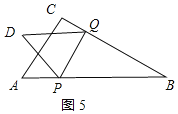
∴∠BQP=180°-∠QPB-∠B=180°-60°-30°=90°,
∴BQ=sin60°PB,即![]()
解得:![]()
②当PQ平分∠DQB时,如图6所示: 则∠PQB=∠DPQ=60°,
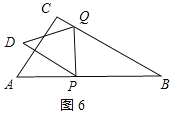
∴∠BPQ=180°-∠PQB-∠B=180°-60°-30°=90°,
∴PB=sin60°BQ,即![]()
解得:![]() .
.
③当PQ平分∠DQC时,如图7所示: 则点Q与点A重合,∠CAP=∠DAP=60°,

此时,![]()
综上所述,当△ABC与△PQD的边所夹的角被PQ平分时,t的值为![]() 或
或![]() 或
或![]() .
.