题目内容
（2013•厦门）如图，?ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，若AC+BD=24厘米，△OAB的周长是18厘米，则EF=3
3
厘米．分析：根据AC+BD=24厘米，可得出出OA+OB=12cm，继而求出AB，判断EF是△OAB的中位线即可得出EF的长度．
解答：解：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
又∵AC+BD=24厘米，
∴OA+OB=12cm，
∵△OAB的周长是18厘米，
∴AB=6cm，
∵点E，F分别是线段AO，BO的中点，
∴EF是△OAB的中位线，
∴EF=
AB=3cm．
故答案为：3．
∴OA=OC，OB=OD，
又∵AC+BD=24厘米，
∴OA+OB=12cm，
∵△OAB的周长是18厘米，
∴AB=6cm，
∵点E，F分别是线段AO，BO的中点，
∴EF是△OAB的中位线，
∴EF=
| 1 |
| 2 |
故答案为：3．
点评：本题考查了三角形的中位线定理，解答本题需要用到：平行四边形的对角线互相平分，三角形中位线的判定定理及性质．
练习册系列答案
相关题目
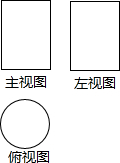（2013•厦门）如图是下列一个立体图形的三视图，则这个立体图形是（ ）
（2013•厦门）如图所示，在⊙O中，
（2013•厦门）如图，在△ABC中，DE∥BC，AD=1，AB=3，DE=2，则BC=
（2013•厦门）如图，在平面直角坐标系中，点O是原点，点B（0，
（2013•厦门）如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点E．若AE=4，CE=8，DE=3，梯形ABCD的高是