题目内容
 (2013•厦门)如图,在平面直角坐标系中,点O是原点,点B(0,
(2013•厦门)如图,在平面直角坐标系中,点O是原点,点B(0,| 3 |
1
1
,| 3 |
| 3 |
分析:根据点B的坐标求出OB的长,再连接ME,根据轴对称的性质可得OB=OE,再求出AO的长度,然后利用勾股定理列式求出AB的长,利用∠A的余弦值列式求出AM的长度,再求出BM的长,然后写出点M的坐标即可.
解答: 解:∵点B(0,
解:∵点B(0,
),
∴OB=
,
连接ME,
∵点B和点E关于直线OM对称,
∴OB=OE=
,
∵点E是线段AO的中点,
∴AO=2OE=2
,
根据勾股定理,AB=
=
=3,
tan∠A=
=
,
即
=
,
解得AM=2,
∴BM=AB-AM=3-2=1,
∴点M的坐标是(1,
).
故答案为:(1,
).
 解:∵点B(0,
解:∵点B(0,| 3 |
∴OB=
| 3 |
连接ME,
∵点B和点E关于直线OM对称,
∴OB=OE=
| 3 |
∵点E是线段AO的中点,
∴AO=2OE=2
| 3 |
根据勾股定理,AB=
| AO2-OB2 |
(2
|
tan∠A=
| AE |
| AM |
| AB |
| AO |
即
| ||
| AM |
| 3 | ||
2
|
解得AM=2,
∴BM=AB-AM=3-2=1,
∴点M的坐标是(1,
| 3 |
故答案为:(1,
| 3 |
点评:本题考查了轴对称的性质,坐标与图形性质,解直角三角形,熟练掌握轴对称的性质并作出辅助线构造出直角三角形是解题的关键.

练习册系列答案
相关题目
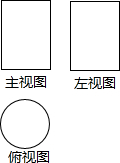 (2013•厦门)如图是下列一个立体图形的三视图,则这个立体图形是( )
(2013•厦门)如图是下列一个立体图形的三视图,则这个立体图形是( ) (2013•厦门)如图所示,在⊙O中,
(2013•厦门)如图所示,在⊙O中,
 (2013•厦门)如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC=
(2013•厦门)如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC= (2013•厦门)如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点E.若AE=4,CE=8,DE=3,梯形ABCD的高是
(2013•厦门)如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点E.若AE=4,CE=8,DE=3,梯形ABCD的高是