题目内容
15.抛物线y=x2+x-4与直线y=2的交点坐标为(-3,2)(2,2).分析 根据函数值,可得相应的自变量的值,根据自变量以相应的函数值,可得点的坐标.
解答 解:当y=2时,x2+x-4=2.
解得x=-3,x=2,
抛物线y=x2+x-4与直线y=2的交点坐标为(-3,2)(2,2).
故答案为:(-3,2)(2,2).
点评 本题考查了二次函数的性质,利用函数值得出相应自变量的值是解题关键.

练习册系列答案
相关题目
5.若反比例函数为y=$\frac{-2}{x}$,则这个函数的图象位于( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
4.菱形的两条对角线长分别为6cm和8cm,则此菱形的面积为( )cm2.
| A. | 14 | B. | 20 | C. | 24 | D. | 48 |
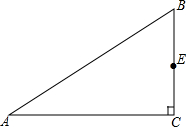 已知,如图,△ABC中,∠C=90°,E为BC边中点.
已知,如图,△ABC中,∠C=90°,E为BC边中点.