题目内容
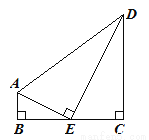
如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
题目内容
如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.

 应用题作业本系列答案
应用题作业本系列答案