题目内容
(12分)如图,在Rt△ABC中,∠C=90°,以BC为直径作⊙O交AB于点D,取AC的中点E,连结DE、OE.

(1)求证:DE是⊙O的切线;(2)如果⊙O的半径是1.5cm,ED=2cm,求AB的长.
(1)详见解析;(2)5cm.
【解析】
试题分析:(1)可证明DE是⊙O的切线,只要证得∠ODE=90°即可.
(2)先利用勾股定理求出OE的长,再利用中位线定理,可求出AB的长.
试题解析:证明:(1)连结OD.
由O、E分别是BC、AC中点得OE∥AB.
∴∠1=∠2,∠B=∠3,又OB=OD.
∴∠2=∠3.
而OD=OC,OE=OE
∴△OCE≌△ODE.
∴∠OCE=∠ODE.
又∠C=90°,故∠ODE =90°.
∴DE是⊙O的切线.
(2)在Rt△ODE中,由OD=1.5,DE=2,
得OE=2.5,
又∵O、E分别是CB、CA的中点,
∴AB=2×OE=2×2.5=5,
∴所求AB的长是5cm.

考点:1、三角形全等的判定和性质;2、切线的判定;3、三角形的中位线定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 时,原方程应变形为( )
时,原方程应变形为( ) B、
B、 C、
C、 D、
D、
 是二次函数,则m=______.
是二次函数,则m=______. 的顶点坐标是( )
的顶点坐标是( )
 的方程
的方程 .
.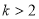 时,方程总有两个不相等的实数根;
时,方程总有两个不相等的实数根; 的图象与x轴交于A,B两点(A在B的左侧),与
的图象与x轴交于A,B两点(A在B的左侧),与 轴交于点C,且tan∠OAC=4,求该二次函数的解析式;
轴交于点C,且tan∠OAC=4,求该二次函数的解析式; 的图象于点N.若只有当
的图象于点N.若只有当 时,点M位于点N的下方,求一次函数
时,点M位于点N的下方,求一次函数 的解析式.
的解析式.
 ,另两条直线分别交
,另两条直线分别交 ,
, ,
, 于点
于点 及点
及点 ,且
,且 ,
, ,
, ,那么下列等式正确的是( )
,那么下列等式正确的是( )
 B.
B.
 D.
D.