题目内容
△ABC的周长为60,∠C等于90°,tanA= ,则△ABC的面积为________.
,则△ABC的面积为________.
150
分析:由△ABC中,∠C等于90°,tanA= ,则可得
,则可得 =
= ,然后设BC=3x,AC=4x,由勾股定理即可求得AB=5x,又由△ABC的周长为60,即可求得各边的长,继而求得△ABC的面积.
,然后设BC=3x,AC=4x,由勾股定理即可求得AB=5x,又由△ABC的周长为60,即可求得各边的长,继而求得△ABC的面积.
解答: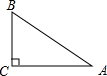 解:∵△ABC中,∠C=90°,tanA=
解:∵△ABC中,∠C=90°,tanA= ,
,
∴ =
= ,
,
设BC=3x,AC=4x,
∴AB= =5x,
=5x,
∵△ABC的周长为60,
∴3x+4x+5x=60,
解得:x=5,
∴AC=20,BC=15,
∴S△ABC= AC•BC=
AC•BC= ×20×15=150.
×20×15=150.
故答案为:150.
点评:此题考查了解直角三角形的知识.此题难度不大,注意数形结合思想与方程思想的应用.
分析:由△ABC中,∠C等于90°,tanA=
 ,则可得
,则可得 =
= ,然后设BC=3x,AC=4x,由勾股定理即可求得AB=5x,又由△ABC的周长为60,即可求得各边的长,继而求得△ABC的面积.
,然后设BC=3x,AC=4x,由勾股定理即可求得AB=5x,又由△ABC的周长为60,即可求得各边的长,继而求得△ABC的面积.解答:
 解:∵△ABC中,∠C=90°,tanA=
解:∵△ABC中,∠C=90°,tanA= ,
,∴
 =
= ,
,设BC=3x,AC=4x,
∴AB=
 =5x,
=5x,∵△ABC的周长为60,
∴3x+4x+5x=60,
解得:x=5,
∴AC=20,BC=15,
∴S△ABC=
 AC•BC=
AC•BC= ×20×15=150.
×20×15=150.故答案为:150.
点评:此题考查了解直角三角形的知识.此题难度不大,注意数形结合思想与方程思想的应用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目