题目内容
3.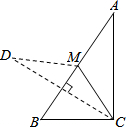 已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,CD恰好与AB垂直,求∠A的度数.
已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,CD恰好与AB垂直,求∠A的度数.
分析 如图,首先证明∠A=∠MCA(设为α);其次证明∠DCM=∠MCA=α;运用直角三角形的两锐角互余,列出关于α的方程,求出α即可解决问题.
解答  解:如图,∵CM是斜边AB上的中线,
解:如图,∵CM是斜边AB上的中线,
∴CM=AM=$\frac{1}{2}$AB,
∴∠A=∠MCA(设为α);
由翻折变换的性质得:∠DCM=∠MCA=α;
∵CD⊥AB,
∴∠DCA+∠A=90°,
即3α=90°,
∴∠A=α=30°.
点评 该题主要考查了翻折变换的性质、直角三角形的性质等几何知识点及其应用问题;应牢固掌握翻折变换的性质等几何知识点,并能灵活运用、解题.

练习册系列答案
相关题目
12.若5x=2,5y=$\frac{1}{2}$,则x,y之间的关系为( )
| A. | x,y互为相反数 | B. | x,y互为倒数 | C. | x=y | D. | 无法判断 |
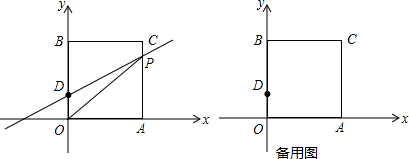
 如图,小敏从A处出发沿南偏东65°方向行走至B处,又沿北偏西15°方向行走至C处,则∠ABC的度数是50°.
如图,小敏从A处出发沿南偏东65°方向行走至B处,又沿北偏西15°方向行走至C处,则∠ABC的度数是50°. 如图,CD是线段AB上两点,若CB=4cm,DB=7cm,且D是AC中点,则AC的长等于6cm.
如图,CD是线段AB上两点,若CB=4cm,DB=7cm,且D是AC中点,则AC的长等于6cm. 如图.在△ABC中,DE∥BC,M为DE上的点,且BM平分∠ABC,CM平分∠ACB.若BD=6,CE=4.则DE=10.
如图.在△ABC中,DE∥BC,M为DE上的点,且BM平分∠ABC,CM平分∠ACB.若BD=6,CE=4.则DE=10.


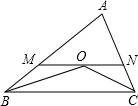 已知:在△ABC中,AB=8cm,AC=6cm,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N,那么△AMN的周长=14cm.
已知:在△ABC中,AB=8cm,AC=6cm,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N,那么△AMN的周长=14cm.