Question

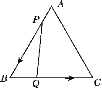
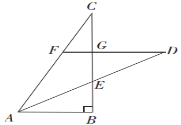
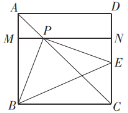
【题目】如图，P是边长为1的正方形ABCD的对角线AC上一动点（不与A、C两点重合），连接BP，过点P作PE⊥PB交直线CD于点E，连接BE，MN//BC分别交AB、DC于点M、N.设.

（1）当点E在CD边上时，线段PE于线段PB有怎样的数量关系？试证明你的结论.

（2）设以点B，C，P，E为顶点的四边形的面积为y，试确定y与x之间的函数关系式，并求出自变量x的取值范围.

Answer 1

【答案】（1）结论：，证明见解析；（2）当点E在线段CD上时，；

当点E在线段DC的延长线上时，.

【解析】

（1）根据正方形的性质可得出.再根据同角的余角相等得出，从而证明≌，即可得证。

（2）分两种情形分别求解：①当点E在线段CD上时，，分别表示出△PBC于△PCE的面积就可以．②当点E在DC的延长线上时，同法可求；

⑴结论：.

证明：在正方形ABCD中，AC为对角线，

∴，

又∵，

∴.

∵，

∴，

又∵，

∴.

在和中，

∵，

∴≌，

∴.

⑵①当点E在线段CD上时，

∵，

设，

∴，，

∴，

又∵，

，

∴，

即.

②如图，当点E在线段DC的延长线上时，

即.

综上所述，当点E在线段CD上时，；

当点E在线段DC的延长线上时，.