题目内容
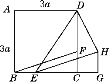
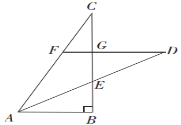
【题目】如图,在△ABC中,∠ABC=90°,且BC=6,AB=3,AD是∠BAC的平分线,与BC相交于点E,点G是BC上一点,E为线段BG的中点,DG⊥BC于点G,交AC于点F,则FG的长为_____.
【答案】![]()
【解析】
先根据∠ABC=90°,DG⊥BC得出DF//AB,再根据E为线段BG的中点,得出![]() ABE
ABE![]() DGE,证出DG=AB=3,再根据AD是∠BAC的平分线,DF//AB,得出DF=AF,再根据
DGE,证出DG=AB=3,再根据AD是∠BAC的平分线,DF//AB,得出DF=AF,再根据![]() CFG
CFG![]() CAB,得出
CAB,得出![]() =
=![]() 即可求出FG。
即可求出FG。
∵∠ABC=90°,DG⊥BC,∴∠ABC=∠DGE,
∴DF//AB, ∴∠D=∠DAB
∵AD是∠BAC的平分线,
∴∠FAD=∠D, ∴AF=DF,
∵E为线段BG的中点,
∴GE=BE,
在![]() ABE和
ABE和![]() DGE中,
DGE中,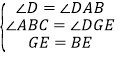
∴![]() ABE
ABE![]() DGE, ∴DG=AB=3,
DGE, ∴DG=AB=3,
设FG=x,则AF=DF=3+x
在△ABC中,∠ABC=90°,且BC=6,AB=3,
根据勾股定理可得:AC=3![]() , 则FC=3
, 则FC=3![]() -3-x
-3-x
∵DF//AB, ∴![]() CFG
CFG![]() CAB,
CAB,
∴![]() =
=![]() ∴
∴![]() =
=![]()
∴x=![]()
∴FG=![]()
故答案为:![]()

练习册系列答案
相关题目