题目内容
14. 如图,已知△ABC中,AB=$2\sqrt{5}$,AC=$4\sqrt{5}$,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
如图,已知△ABC中,AB=$2\sqrt{5}$,AC=$4\sqrt{5}$,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
分析 作MN∥BC交AC于点N,利用三角形的中位线定理可得MN的长;作∠ANM=∠B,利用相似可得MN的长.
解答 解:①图1,作MN∥BC交AC于点N,则△AMN∽△ABC,
有$\frac{AM}{AB}=\frac{MN}{BC}$,
∵M为AB中点,AB=$2\sqrt{5}$,
∴AM=$\sqrt{5}$,
∵BC=6,
∴MN=3;
②图2,作∠ANM=∠B,则△ANM∽△ABC,
有$\frac{AM}{AC}=\frac{MN}{BC}$,
∵M为AB中点,AB=$2\sqrt{5}$,
∴AM=$\sqrt{5}$,
∵BC=6,AC=$4\sqrt{5}$,
∴MN=$\frac{3}{2}$,
∴MN的长为3或$\frac{3}{2}$.
点评 本题主要考查相似三角形的作图和相似三角形的判定以及存在性,解题的关键是注意相似作图及解答有多种情况.

练习册系列答案
相关题目
5.直角坐标系中点P(a+2,a-2)不可能所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.若a<b<0,则下列结论中错误的是( )
| A. | b-a>0 | B. | $\frac{a}{b}$>1 | C. | a-3<b-3 | D. | 5-a<5-b |
3.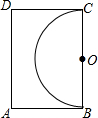 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )| A. | 9m | B. | 7m | C. | 5m | D. | 3m |
4.把点(2,-3)先向左平移3个单位长度,再向下平移2个单位长度得到的点的坐标是( )
| A. | (-1,-5) | B. | (5,-1) | C. | (5,-5) | D. | (-1,-1) |

 如图,∠ABD=125°,∠A=50°,则∠ACE的度数是105°.
如图,∠ABD=125°,∠A=50°,则∠ACE的度数是105°.