题目内容
 如图,以点M(5,3)为圆心的⊙M切y轴于点A,与x轴交于B(1,0),C两点(点B在点C的左侧),直线l过圆心M且垂直于y轴,点P是直线l上的一个动点,如果△PAB的周长最小,那么此时点P的坐标是________.
如图,以点M(5,3)为圆心的⊙M切y轴于点A,与x轴交于B(1,0),C两点(点B在点C的左侧),直线l过圆心M且垂直于y轴,点P是直线l上的一个动点,如果△PAB的周长最小,那么此时点P的坐标是________.
(5, )
)
分析:连接AM,由切线的性质可知,AM⊥y轴,根据M点的坐标可求出AM及MD的长,作点A关于直线l的对称点A′,连接A′B,则线段A′B的长即为△PAB的最小周长,再用待定系数法求出直线A′B的解析式,得出此直线与直线l的交点坐标即可.
解答: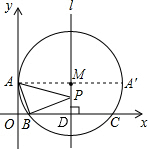 解:连接AM,
解:连接AM,
∵⊙M切y轴于点A,
∴AM⊥y轴,
∵M(5,3),l⊥x轴,
∴AM=5,MD=3,直线l的解析式为l=5,
作点A关于直线l的对称点A′,则A′(10,3),连接A′B,则线段A′B的长即为△PAB的最小周长,
设过点A′、B的直线解析式为y=kx+b(k≠0),则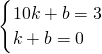 ,解得
,解得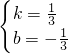 ,
,
∴此直线的解析式为:y= x-
x- ,
,
∴当x=5时,y= ×5-
×5- =
= ,
,
∴点P的坐标是(5, ).
).
故答案为:(5, ).
).
点评:本题考查的是轴对称-最短路线问题,熟知“两点之间,线段最短”的知识是解答此题的关键.
 )
)分析:连接AM,由切线的性质可知,AM⊥y轴,根据M点的坐标可求出AM及MD的长,作点A关于直线l的对称点A′,连接A′B,则线段A′B的长即为△PAB的最小周长,再用待定系数法求出直线A′B的解析式,得出此直线与直线l的交点坐标即可.
解答:
 解:连接AM,
解:连接AM,∵⊙M切y轴于点A,
∴AM⊥y轴,
∵M(5,3),l⊥x轴,
∴AM=5,MD=3,直线l的解析式为l=5,
作点A关于直线l的对称点A′,则A′(10,3),连接A′B,则线段A′B的长即为△PAB的最小周长,
设过点A′、B的直线解析式为y=kx+b(k≠0),则
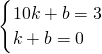 ,解得
,解得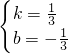 ,
,∴此直线的解析式为:y=
 x-
x- ,
,∴当x=5时,y=
 ×5-
×5- =
= ,
,∴点P的坐标是(5,
 ).
).故答案为:(5,
 ).
).点评:本题考查的是轴对称-最短路线问题,熟知“两点之间,线段最短”的知识是解答此题的关键.

练习册系列答案
相关题目
 如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(-1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系.
如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(-1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系. 26、如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A.EB与AD一定平行吗?为什么?
26、如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A.EB与AD一定平行吗?为什么? 12、如图,以点B为中心,把△ABC旋转180°.
12、如图,以点B为中心,把△ABC旋转180°. 如图,以点O为圆心的两个同心圆,当大圆的弦AB与小圆相切时弦长AB=8,则这两个同心圆所形成的圆环的面积是
如图,以点O为圆心的两个同心圆,当大圆的弦AB与小圆相切时弦长AB=8,则这两个同心圆所形成的圆环的面积是 如图,以点M(5,3)为圆心的⊙M切y轴于点A,与x轴交于B(1,0),C两点(点B在点C的左侧),直线l过圆心M且垂直于y轴,点P是直线l上的一个动点,如果△PAB的周长最小,那么此时点P的坐标是
如图,以点M(5,3)为圆心的⊙M切y轴于点A,与x轴交于B(1,0),C两点(点B在点C的左侧),直线l过圆心M且垂直于y轴,点P是直线l上的一个动点,如果△PAB的周长最小,那么此时点P的坐标是