��Ŀ����
����Ŀ��ijУһ��ǽ![]() ǰ��һ��յأ�У�����ó�
ǰ��һ��յأ�У�����ó�![]() ��դ����
��դ����![]() ��Χ��һ��һ�濿ǽ�ij����λ�Χ���ٽ�������
��Χ��һ��һ�濿ǽ�ij����λ�Χ���ٽ�������![]() �ָ�����飨��ͼ��ʾ�� ����֪
�ָ�����飨��ͼ��ʾ�� ����֪![]() ��
��![]() ��
��![]() ����
����![]() ��
��
��1���ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() ��
��![]() ��
��
��2����������![]() ���������
���������![]() ʱ����
ʱ����![]() �ij���
�ij���
��3��������ͼ�ļ�������ֲ���ܣ��������ְز�ƺ���ְػ��ܵijɱ�Ϊÿƽ����100Ԫ���ֱ���ƺ�ijɱ�Ϊÿƽ����50Ԫ������ֲ�������ƺ���ܷ��ó���6300Ԫ����Χ�Ŀ�![]() �ķ�Χ��
�ķ�Χ��
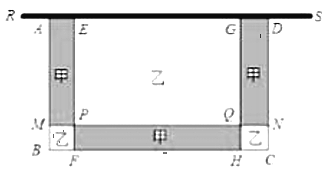
���𰸡���1��![]() ����2��AB�ij�Ϊ
����2��AB�ij�Ϊ![]() ��
��![]() ����3�����ԵĿ�
����3�����ԵĿ�![]() ʱ���ܷ��ó��� 6300 Ԫ��
ʱ���ܷ��ó��� 6300 Ԫ��
��������
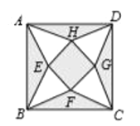
��1�����ݾ��ε����ʿɵ�![]() ������դ�����ܳ�����α߳��Ĺ�ϵ���ɱ�ʾ��
������դ�����ܳ�����α߳��Ĺ�ϵ���ɱ�ʾ��![]() ��������ʾ��
��������ʾ��![]() ��
��
��2���ȱ�ʾ��������![]() �ı߳������ó����ε������ʽ�г����̣���⼴�����AB�ij���
�ı߳������ó����ε������ʽ�г����̣���⼴�����AB�ij���
��3�����������������������������ܷ���Ϊ![]() Ԫ���������г�y����x�Ĺ�ϵʽ�����ö��κ�����������ⲻ��ʽ��������û�Χ�Ŀ�
Ԫ���������г�y����x�Ĺ�ϵʽ�����ö��κ�����������ⲻ��ʽ��������û�Χ�Ŀ�![]() �ķ�Χ��
�ķ�Χ��
�⣺��1�����ı���![]() �Ǿ��Σ�
�Ǿ��Σ�![]() ��
��
��![]() ��
��
������ã�![]() ��
��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��
���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��![]() ��
��
���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��![]() ��
��
���ı���![]() �������Σ���
����������![]() ��
��
ͬ���ã����ı���![]() �������Σ���
����������![]() ��
��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��2����![]() ��
��
������ɵã�![]()
��ã�![]() ��
��
![]() �ij�Ϊ
�ij�Ϊ![]() ��
��![]() ��
��
��3������������![]() ��
��
����������=![]() ��
��
���ܷ���Ϊ![]() Ԫ��������ã�
Ԫ��������ã�
![]() ��
��
�����ã�![]() ��
��
��![]() ����
����![]() ��
��
��ã�![]() ��
��
�ɶ��κ�����ͼ�������ʿɵã��� ![]() ʱ��
ʱ��![]() ��
��
��ԵĿ�![]() ʱ���ܷ��ó��� 6300 Ԫ��
ʱ���ܷ��ó��� 6300 Ԫ��
������ֲ�������ƺ���ܷ��ó���6300Ԫ����Χ�Ŀ�![]() �ķ�ΧΪ
�ķ�ΧΪ![]() ��
��

����Ŀ��Ϊ�˴�С����С��������ѡ��һ�˲μ�����������ֶ����ǵ����ˮƽ���в��ԣ���������ͬ�����¸����6�Σ����еĻ������£���λ��������
����7��8��7��8��9��9�� ����5��8��7��8��10��10��
��1��������
ƽ���������� | ��λ�������� | �����2�� | |
�� | 8 | ||
�� | 8 | 3 |
��2������������Ϣ������Ϊ������ѡ��˭�μӱ�����������ʲô��
��3����С�������2�Σ��ֱ�����7����9������С����8������ɼ��ķ��� �������������������С��������������