题目内容
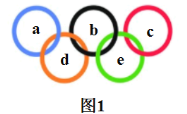
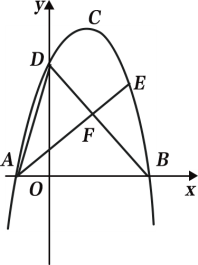
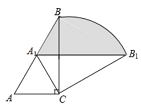
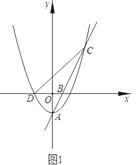
【题目】如图1,抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,直线
,直线![]() 交抛物线W于另一点
交抛物线W于另一点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
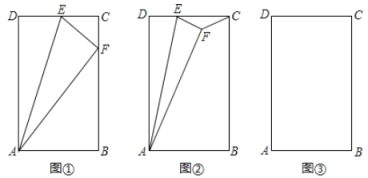
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,若
,若![]() 平分
平分![]() ,求抛物线W的解析式;
,求抛物线W的解析式;
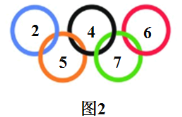
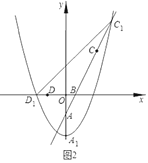
(3)若![]() ,将抛物线W向下平移
,将抛物线W向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,如图2,记抛物线
,如图2,记抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,与射线
,与射线![]() 的交点为
的交点为![]() .问:在平移的过程中,
.问:在平移的过程中,![]() 是否恒为定值?若是,请求出
是否恒为定值?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 恒为定值
恒为定值![]() .
.
【解析】
(1)由抛物线解析式可得顶点A坐标为(0,-2),利用待定系数法即可得直线AB解析式;
(2)如图,过点![]() 作
作![]() 于
于![]() ,根据角平分线的性质可得BE=BN,由∠BND=∠CED=90°,∠BND=∠CDE可证明
,根据角平分线的性质可得BE=BN,由∠BND=∠CED=90°,∠BND=∠CDE可证明![]() ,设BE=x,BD=y,根据相似三角形的性质可得CE=2x,CD=2y,根据勾股定理由得y与x的关系式,即可用含x的代数式表示出C、D坐标,代入y=ax2-2可得关于x、a的方程组,解方程组求出a值即可得答案;
,设BE=x,BD=y,根据相似三角形的性质可得CE=2x,CD=2y,根据勾股定理由得y与x的关系式,即可用含x的代数式表示出C、D坐标,代入y=ax2-2可得关于x、a的方程组,解方程组求出a值即可得答案;
(3)过点![]() 作
作![]() 于点
于点![]() ,根据平移规律可得抛物线W1的解析式为y=
,根据平移规律可得抛物线W1的解析式为y=![]() x2-2-m,设点
x2-2-m,设点![]() 的坐标为(t,0)(t<0),代入y=
的坐标为(t,0)(t<0),代入y=![]() x2-2-m可得2+m=
x2-2-m可得2+m=![]() t2,即可的W1的解析式为y=
t2,即可的W1的解析式为y=![]() x2-
x2-![]() t2,联立直线BC解析式可用含t的代数式表示出点C1的坐标,即可得
t2,联立直线BC解析式可用含t的代数式表示出点C1的坐标,即可得![]() ,可得∠
,可得∠![]() ,根据抛物线W的解析式可得点D坐标,联立直线BC与抛物线W的解析式可得点C、A坐标,即可求出CG、DG的长,可得CG=DG,∠CDG=∠
,根据抛物线W的解析式可得点D坐标,联立直线BC与抛物线W的解析式可得点C、A坐标,即可求出CG、DG的长,可得CG=DG,∠CDG=∠![]() ,即可证明
,即可证明![]() ,可得
,可得![]() ,
,![]() ,由∠CDG=45°可得BF=DF,根据等腰三角形的性质可求出DF的长,利用勾股定理可求出CD的长,即可求出CF的长,根据三角函数的定义即可得答案.
,由∠CDG=45°可得BF=DF,根据等腰三角形的性质可求出DF的长,利用勾股定理可求出CD的长,即可求出CF的长,根据三角函数的定义即可得答案.
(1)∵抛物线W:![]() 的顶点为点
的顶点为点![]() ,
,
∴点![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
∵B(1,0),
∴![]() ,
,
解得:![]() ,
,
∴抛物线解析式为:![]() .
.
(2)如图,过点![]() 作
作![]() 于
于![]() ,
,
∵![]() 平分,
平分,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() ,点
,点![]() ,
,
∴点![]() ,点
,点![]() 是抛物线W:
是抛物线W:![]() 上的点,
上的点,
∴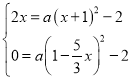 ,
,
∵x>0,
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为:![]() .
.
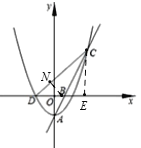
(3)![]() 恒为定值,理由如下:
恒为定值,理由如下:
如图,过点![]() 作
作![]() 轴于H,过点
轴于H,过点![]() 作
作![]() 轴G,过点
轴G,过点![]() 作
作![]() 于点
于点![]() ,
,
∵a=![]() ,
,
∴抛物线W的解析式为y=![]() x2-2,
x2-2,
∵将抛物线W向下平移m个单位,得到抛物线![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() ,
,
∵抛物线![]() 与射线
与射线![]() 的交点为
的交点为![]() ,
,
∴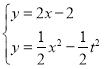 ,
,
解得: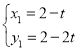 ,
, (不合题意舍去),
(不合题意舍去),
∴点![]() 的坐标
的坐标![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() 轴,
轴,
![]() ,
,
∵![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴点![]() ,
,
∵![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() ,
,
∴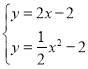 ,
,
解得:![]() 或
或![]() ,
,
∴点![]() ,A(0,-2),
,A(0,-2),
∴![]() ,
,
∴![]() ,且
,且![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() ,点
,点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 恒为定值.
恒为定值.