题目内容
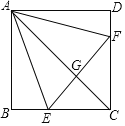
【题目】如图,![]() 是一个锐角三角形,分别以
是一个锐角三角形,分别以![]() 、
、![]() 向外作等边三角形
向外作等边三角形![]() 、
、![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() .
.
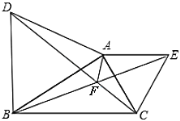
(1)求证:![]()
(2)求证:![]()
【答案】(1)见解析;(2)见解析
【解析】
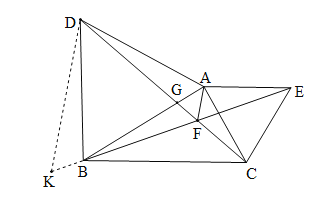
(1)过A作AM⊥CD于M,AN⊥BE于N,设AB与CD相交于点G.根据等边三角形的性质得到AD=AB,AC=AE,∠BAD=∠CAE=60°,根据全等三角形的判定定理即可得△ACD≌△AEB,根据全等三角形的性质可得AM=AN,根据角平分线的判定定理即可得到∠DFA=∠AFE,再根据全等三角形的对应角相等和三角形内角和等于180°得到∠DFB=∠DAG=60°,即可得到结论;
(2)如图,延长FB至K,使FK=DF,连DK,根据等边三角形的性质和全等三角形的判定和性质定理即可得到结论.
(1)过A作AM⊥CD于M,AN⊥BE于N,设AB与CD相交于点G.
∵△ABD和△ACE为等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠DAC=∠BAE=60°+∠BAC.
在△ACD和△AEB中,∵ ,
,
∴△ACD≌△AEB,
∴CD=BE,∠ADG=∠ABF,△ADC的面积=△ABE的面积,
∴![]() CDAM=
CDAM=![]() BEAN,
BEAN,
∴AM=AN,
∴AF是∠DFE的平分线,
∴∠DFA=∠AFE.
∵∠ADG=∠ABF,∠AGD=∠BGF,
∴∠DFB=∠DAG=60°,
∴∠GFE=120°,
∴∠BFD=∠DFA=∠AFE.
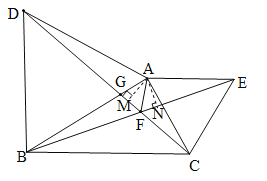
(2)如图,延长FB至K,使FK=DF,连接DK.
∵∠DFB=60°,
∴△DFK为等边三角形,
∴DK=DF,∠KDF=∠K=60°,
∴∠K=∠DFA=60°.
∵∠ADB=60°,
∴∠KDB=∠FDA.
在△DBK和△DAF中,
∵∠K=∠DFA,DK=DF,∠KDB=∠FDA,
∴△DBK≌△DAF,
∴BK=AF.
∵DF=DK=FK=BK+BF,
∴DF=AF+BF,
又∵CD=DF+CF,
∴CD=AF+BF+CF.