题目内容
如图,已知△ABC内接于⊙O,过A作⊙O的切线,与BC的延长线交于D,且AD=| 3 |
 =2,∠ADC=30°
=2,∠ADC=30°(1)AC与BC的长;
(2)求∠ABC的度数;
(3)求弓形AmC的面积.
分析:(1)作CE⊥AD于E,则CE=1,利用角边关系又可求出AE,AC,BC的长;
(2)利用三角形的内角和是180度,可求出∠ABC的度数;
(3)仔细观察图形可得S弓形AmC=S扇形OAmC-S△AOC,然后利用面积公式进行计算.
(2)利用三角形的内角和是180度,可求出∠ABC的度数;
(3)仔细观察图形可得S弓形AmC=S扇形OAmC-S△AOC,然后利用面积公式进行计算.
解答: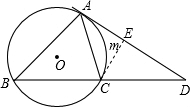 解:(1)作CE⊥AD于E,
解:(1)作CE⊥AD于E,
∴CE=1,DE=
,
又∵AD=
+1,
∴AE=1,AC=
,
∴∠ABC=45°,
又∵AD2=CD•BD,
∴BC=
;
(2)∵∠ADC=30°,
∴∠ECD=60°,
∴∠AFD=60°,
∴∠ABC=30°;
(3)S弓形AmC=S扇形OAmC-S△AOC=
π-
,
∴AC=
,BC=
,∠ABC=45°,
∴S弓形AmC=
π-
.
 解:(1)作CE⊥AD于E,
解:(1)作CE⊥AD于E,∴CE=1,DE=
| 3 |
又∵AD=
| 3 |
∴AE=1,AC=
| 2 |
∴∠ABC=45°,
又∵AD2=CD•BD,
∴BC=
| 3 |
(2)∵∠ADC=30°,
∴∠ECD=60°,
∴∠AFD=60°,
∴∠ABC=30°;
(3)S弓形AmC=S扇形OAmC-S△AOC=
| 1 |
| 4 |
| 1 |
| 2 |
∴AC=
| 2 |
| 3 |
∴S弓形AmC=
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题综合考查了解直角三角形,及扇形的三角形的面积公式.

练习册系列答案
相关题目
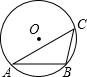 如图,已知△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为
如图,已知△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为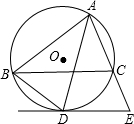 如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.
如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E. (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N. 如图,已知△ABC内接于⊙O,AE平分∠BAC,且AD⊥BC于点D,连接OA.
如图,已知△ABC内接于⊙O,AE平分∠BAC,且AD⊥BC于点D,连接OA. 如图,已知△ABC内接于⊙O,AB=AC,∠A=36°,CD是⊙O的直径,求∠ACD的度数.
如图,已知△ABC内接于⊙O,AB=AC,∠A=36°,CD是⊙O的直径,求∠ACD的度数.