题目内容
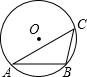如图，已知△ABC内接于⊙O，∠C=45°，AB=4，则⊙O的半径为分析：连接OA，OB，根据一条弧所对的圆周角等于它所对的圆心角的一半，得∠AOB=90°，又OA=OB，AB=4，根据勾股定理，得圆的半径是2
．
| 2 |
解答：
解：连接OA，OB
∵∠C=45°
∴∠AOB=90°
又∵OA=OB，AB=4
∴OA=2
．
解：连接OA，OB∵∠C=45°
∴∠AOB=90°
又∵OA=OB，AB=4
∴OA=2
| 2 |
点评：此题运用了圆周角定理以及勾股定理．
练习册系列答案
智慧小复习系列答案
相关题目
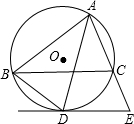如图，已知△ABC内接于⊙O，AD平分∠BAC，交⊙O于点D，过D作⊙O的切线与AC的延长线交于点E．
（2013•樊城区模拟）如图，已知△ABC内接于⊙O，弦AD交BC于E，过点D的切线MN交直线AB于M，交直线AC于N．
如图，已知△ABC内接于⊙O，AE平分∠BAC，且AD⊥BC于点D，连接OA．
如图，已知△ABC内接于⊙O，AB=AC，∠A=36°，CD是⊙O的直径，求∠ACD的度数．