题目内容
6. 如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,请你补充一个条件,当BP=2PC时,能够使△ABP与△ECP相似.
如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,请你补充一个条件,当BP=2PC时,能够使△ABP与△ECP相似.
分析 设AB=4x,用x表示出EC、BP、PC,根据相似三角形的判定定理解答即可.
解答 解:当BP=2PC时,△ABP∽△ECP,
设AB=4x,则EC=2x,
∵BP=2PC,
∴BP=$\frac{8}{3}$x,PC=$\frac{4}{3}$x,
则$\frac{AB}{EC}$=2,$\frac{BP}{PC}$=2,
∴$\frac{AB}{EC}$=$\frac{BP}{PC}$,又∠B=∠C=90°,
∴△ABP∽△ECP,
故答案为:BP=2PC.
点评 本题考查的是相似三角形的判定、正方形的性质,掌握相似三角形的判定定理是解题的关键.

练习册系列答案
相关题目
16.二次函数y=-x2+6x-9的图象与x轴的交点坐标为( )
| A. | (2,0) | B. | (0,2) | C. | (0,3) | D. | (3,0) |
14.对一个三角形进行折叠,折痕是这个三角形角平分线的是( )
| A. |  | B. |  | C. |  | D. |  |


 如图所示,已知数 a,b,c 在数轴上对应点的位置:化简|a-b|+|b-c|得2b-a-c.
如图所示,已知数 a,b,c 在数轴上对应点的位置:化简|a-b|+|b-c|得2b-a-c.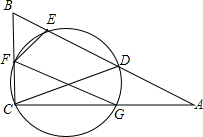 如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG.
如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG.