题目内容
如图，在矩形ABCD中，AB=5，BC=7，点E为BC上一动点，把△ABE沿AE折叠，当点B的对应点B′落在∠ADC的角平分线上时，则点B′到BC的距离为（ ）
A．1或2 B． 2或3 C． 3或4 D． 4或5
A： 解：如图，连接B′D，过点B′作B′M⊥AD于M．
∵点B的对应点B′落在∠ADC的角平分线上，
∴设DM=B′M=x，则AM=7﹣x，
又由折叠的性质知AB=AB′=5，
∴在直角△AMB′中，由勾股定理得到：AM2=AB′2﹣B′M2
即（7﹣x）2=25﹣x2，
解得x=3或x=4，
则点B′到BC的距离为2或1．
故选：A．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
=
；
mm C． 6mm D． 6
活动，随机调查了部分学生对湟鱼洄游的了解程度，以下是根据调查结果做出的统计图的一部分：
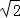=1.41，
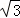=1.73）．