题目内容
12. 如图,四边形ABCD各顶点的坐标分别是A(0,0),B(8,0),C(6,4),D(3,6),求出四边形ABCD的面积.
如图,四边形ABCD各顶点的坐标分别是A(0,0),B(8,0),C(6,4),D(3,6),求出四边形ABCD的面积.
分析 本题应利用分割法,把四边形分割成两个三角形加上一个梯形后再求面积.
解答 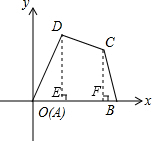 解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:
解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:
S=S△OED+SEFCD+S△CFB
=$\frac{1}{2}$×AE×DE+$\frac{1}{2}$×(CF+DE)×EF+$\frac{1}{2}$×FC×FB.
=$\frac{1}{2}$×3×6+$\frac{1}{2}$×(4+6)×3+$\frac{1}{2}$×2×4
=28.
故四边形ABCD的面积为28.
点评 此题主要考查了点的坐标的意义以及与图形相结合的具体运用.要掌握两点间的距离公式和图形有机结合起来的解题方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列各式,①-(-2); ②-|-2|; ③-23; ④-(-2)2.计算结果为负数的个数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.将抛物线y=2x2向左平移2个单位,再向上平移3个单位得到的抛物线解析式是( )
| A. | y=2(x+2)2+3 | B. | y=2(x-2)2-3 | C. | y=2(x+2)2-3 | D. | y=2(x-2)2+3 |
 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论: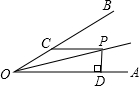 如图所示,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PC=4,则PD的长为( )
如图所示,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PC=4,则PD的长为( ) 如图所示,是一个简单几何体的三视图,则这个几何体的侧面积等于18.
如图所示,是一个简单几何体的三视图,则这个几何体的侧面积等于18.