题目内容
 反比例函数y=
反比例函数y=| k |
| x |
分析:先设反比例函数的解析式为y=
(k≠0),根据△POQ的面积为1,得出
|k|=1,k=±2,再根据反比例函数y=
在第一象限内,即可求出k.
| k |
| x |
| 1 |
| 2 |
| k |
| x |
解答:解:设反比例函数的解析式为y=
(k≠0),
∵△POQ的面积为1,
∴
|k|=1,
|k|=2,
k=±2,
∵反比例函数y=
在第一象限内,
∴k=2;
故选:B.
| k |
| x |
∵△POQ的面积为1,
∴
| 1 |
| 2 |
|k|=2,
k=±2,
∵反比例函数y=
| k |
| x |
∴k=2;
故选:B.
点评:此题考查了反比例函数y=
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得三角形面积为
|k|,体现了数形结合的思想,要正确理解k的几何意义.
| k |
| x |
| 1 |
| 2 |

练习册系列答案
相关题目
 反比例函数y=
反比例函数y=| k |
| x |
| A、1 | B、2 | C、3 | D、4 |
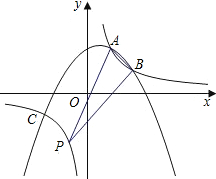 如图,抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和C(-2,-1)三点.
如图,抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和C(-2,-1)三点. 如图,L1是反比例函数y=
如图,L1是反比例函数y= 如图,m是反比例函数y=
如图,m是反比例函数y= (2013•铁岭)如图,点P是正比例函数y=x与反比例函数y=
(2013•铁岭)如图,点P是正比例函数y=x与反比例函数y=