Question

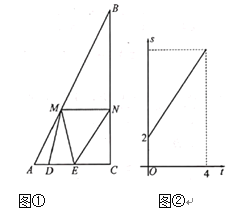
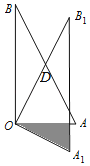
【题目】如图，在△OAB中，∠AOB＝90°，AO＝2，BO＝4．将△OAB绕顶点O按顺时针方向旋转到△OA1B1处，此时线段OB1与AB的交点D恰好为线段AB的中点，线段A1B1与OA交于点E，则图中阴影部分的面积__．

Answer 1

【答案】．

【解析】

根据题意求出△AOB的面积，在根据直角三角形斜边中线的性质得出OD＝BD＝AD，从而判断出∠ODA＝∠OAD，再根据旋转的性质和勾股定理，得出A1O和OE的长度，再根据三角形面积公式计算求解即可.

如图，

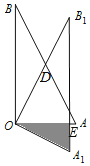
∵∠AOB＝90°，AO＝2，BO＝4，

∴S△AOB＝×2×4＝4，AB＝＝＝2，

∵∠AOB＝90°，点D是AB中点，

∴OD＝BD＝AD，

∴∠ODA＝∠OAD，

∵将△OAB绕顶点O按顺时针方向旋转到△OA1B1处，

∴∠B＝∠B1，S△AOB＝＝4，A1O＝AO＝2，

∵∠B+∠OAD＝90°，

∴∠B1+∠AOD＝90°，

∴∠OEB1＝90°，

∴＝4＝×2×OE，

∴OE＝，

∴A1E＝＝＝，

∴图中阴影部分的面积＝××＝，

故答案为：