题目内容
在平面直角坐标系中,已知点A(a,0),C(0,b)满足(a+1)2+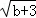 =0
=0
(1)直接写出:a= _________ ,b= _________ ;
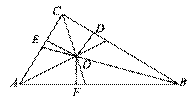
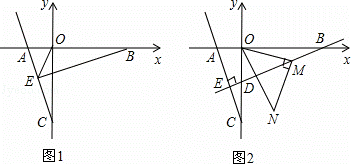
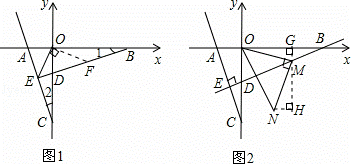
(2)点B为x轴正半轴上一点,如图1,BE⊥AC于点E,交y轴于点D,连接OE,若OE平分∠AEB,求直线BE的解析式;
(3)在(2)条件下,点M为直线BE上一动点,连OM,将线段OM逆时针旋转90°,如图2,点O的对应点为N,当点M的运动轨迹是一条直线l,请你求出这条直线l的解析式.
考点:
一次函数综合题.
分析:
(1)根据非负数是性质来求a、b的值;
(2)如图1,过点O作OF⊥OE,交BE于F.构建全等三角形:△EOC≌△FOB(ASA),△AOC≌△DOB(ASA),易求D(0,﹣1),B(3,0).利用待定系数法求得直线BE的解析式y=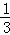 x﹣1;
x﹣1;
(3)如图2,过点M作MG⊥x轴,垂足为G,过点N作NH⊥GH,垂足为H.构建全等三角形:△GOM≌△HMN,故OG=MH,GM=NH.设M(m,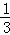 m﹣1),则H(m,﹣
m﹣1),则H(m,﹣ m﹣1),
m﹣1),
N(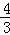 m﹣1,﹣
m﹣1,﹣ m﹣1),由此求得点N的横纵坐标间的函数关系.
m﹣1),由此求得点N的横纵坐标间的函数关系.
解答:
解:(1)依题意得 a+1=0,b+3=0,
解得 a=﹣1,b=﹣3.
故答案是:﹣1;﹣3;
(2)如图1,过点O作OF⊥OE,交BE于F.
∵BE⊥AC,OE平分∠AEB,
∴△EOF为等腰直角三角形.
∵在△EOC与△FOB中, ,
,
∴△EOC≌△FOB(ASA),
∴OB=OC.
∴在△AOC与△DOB中,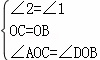 ,
,
∴△AOC≌△DOB(ASA),
∴OA=OD,
∵A(﹣1,0),B(0,﹣3),∴D(0,﹣1),B(3,0)
∴直线BD,即直线BE的解析式y=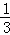 x﹣1;
x﹣1;
(3)依题意,△NOM为等腰Rt△,
如图2,过点M作MG⊥x轴,垂足为G,过点N作NH⊥GH,垂足为H,
∵△NOM为等腰Rt△,
则易证△GOM≌△HMN,
∴OG=MH,GM=NH,
由(2)知直线BD的解析式y=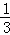 x﹣1,
x﹣1,
设M(m,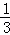 m﹣1),则H(m,﹣
m﹣1),则H(m,﹣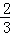 m﹣1),
m﹣1),
∴N(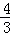 m﹣1,﹣
m﹣1,﹣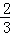 m﹣1),
m﹣1),
令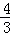 m﹣1=x,﹣
m﹣1=x,﹣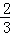 m﹣1=y,
m﹣1=y,
消去参数m得,y=﹣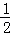 x﹣
x﹣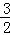
即直线l的解析式为y=﹣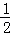 x﹣
x﹣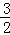 .
.
(说明:此题用取特殊点计算的方法求解析式也行)
点评:
本题考查了一次函数综合题型.熟练掌握等腰直角三角形的性质、全等三角形的判定与性质以及旋转的性质.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案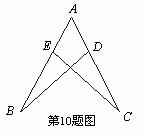 A.∠B=∠C B.AD=AE C.∠BDC=∠CEB D.BD=CE
A.∠B=∠C B.AD=AE C.∠BDC=∠CEB D.BD=CE BC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC等于( ).
BC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC等于( ).

 (D)
(D)