题目内容
【题目】如图,四边形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半抽上,点
轴的正半抽上,点![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿线段
个单位长度的速度沿线段![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线
的垂线![]() 交线段
交线段![]() 于点
于点![]() ,以线段
,以线段![]() 为斜边向右作等腰直角
为斜边向右作等腰直角![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ).
).
(1) 点F的坐标为( , )点![]() 的坐标为( , )(用含
的坐标为( , )(用含![]() 的代数式表示),
的代数式表示),
(2)连接![]() 、
、![]() ,当
,当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)设点![]() 从点
从点![]() 出发时,点
出发时,点![]() 、
、![]() 、
、![]() 都与点
都与点![]() 重合,点
重合,点![]() 在运动过程中,当
在运动过程中,当![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 运动的时间
运动的时间![]() 的值﹒
的值﹒
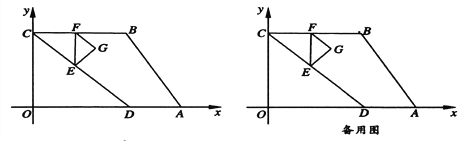
【答案】(1) G(![]() ); (2) t=2或t=
); (2) t=2或t=![]() -2;(3)见解析.
-2;(3)见解析.
【解析】
根据等腰直角三角形的性质和勾股定理,求出CF=EF=t,然后表示出F点的坐标,再根据直角三角形斜边上的中线等于斜边的一半,求出G的坐标;
(2)根据相似三角形的对应边相等,分类讨论求出t的值即可;
(3)求出直线AB的解析式,过点G作x轴的平行线交AB于点H,根据点G的坐标求出H的坐标,根据三角形的面积求解即可.
(1)∵OC=OD=4
∴∠OCD=45°
∵CE=![]() t,
t,
∴CF=FE=t
∴F点为(t,4)
∵△EFG是等腰直角三角形,
∴G点到y轴的距离为![]() t
t
即G(![]() );
);
(2) ∵CE=![]() , ∴EF=CF=t,FG=
, ∴EF=CF=t,FG=![]() ,BF=4-t, ∵∠OCE=∠BFG=45°, ①若△OCE∽△BFG,则
,BF=4-t, ∵∠OCE=∠BFG=45°, ①若△OCE∽△BFG,则![]() ,即
,即![]() ,解得t=2; ②若△ECO∽BFG,则
,解得t=2; ②若△ECO∽BFG,则![]() ,即
,即 ![]() ,解得t=
,解得t=![]() -2;综上所述,当t=2或t=
-2;综上所述,当t=2或t=![]() -2时,以C 、E 、O 为顶点的三角形与 相似.
-2时,以C 、E 、O 为顶点的三角形与 相似.
(3)设直线AB的方程为y=kx+b,则![]() ,解得
,解得![]() ,∴y=-2x+12,
,∴y=-2x+12,

过点G作x轴的平行线交AB于点H, ∵点G的坐标为(![]() ),将y=4-
),将y=4-![]() 代入y=-2x+12得x=4+
代入y=-2x+12得x=4+![]() ,∴点H的坐标为(
,∴点H的坐标为(![]() ),
),![]() ,由2
,由2![]() ,得t=
,得t=![]() 或t=
或t=![]() (舍去).
(舍去).

练习册系列答案
相关题目