题目内容
 如图,平行四边形ABCD中,AE⊥BC,AN⊥CD,垂足分别为E、N,且AE=BE,AN、BD交于点O,∠ADB=15°,问:DF=2
如图,平行四边形ABCD中,AE⊥BC,AN⊥CD,垂足分别为E、N,且AE=BE,AN、BD交于点O,∠ADB=15°,问:DF=2| 2 |
考点:平行四边形的判定与性质,勾股定理
专题:证明题
分析:先回答成立,然后根据题意作辅助线,构造出平行四边形进而即可根据线段的关系进行推理得证.
解答:解:DF=2
AE成立.理由如下:
如图所示,延长DC、AE相交于点G,连接BG,过点B作BH⊥DG于点H,过点F作FM⊥DG于点M,
∴四边形ABHN是平行四边形,
∴BH=AN,
∵∠BDC=∠ADC-∠ADB=30°,
∴BD=2BH=2BN,
∵∠DAG=90°,∠ADG=45°,
∴DG=
AD=
•
AN=2AN,
∴DB=DG,
∴∠DBG=∠DGB=75°,
∴∠EBG=∠FBG-∠DBC=60°,∠BGF=30°,
∴BG=2BE=2AE,∠BFG=75°=∠FBG,
∴FG=BG=2AE,
∵DF=2FM,FG=
FM,
∴DF=
FG=2
AE.

| 2 |
如图所示,延长DC、AE相交于点G,连接BG,过点B作BH⊥DG于点H,过点F作FM⊥DG于点M,
∴四边形ABHN是平行四边形,
∴BH=AN,
∵∠BDC=∠ADC-∠ADB=30°,
∴BD=2BH=2BN,
∵∠DAG=90°,∠ADG=45°,
∴DG=
| 2 |
| 2 |
| 2 |
∴DB=DG,
∴∠DBG=∠DGB=75°,
∴∠EBG=∠FBG-∠DBC=60°,∠BGF=30°,
∴BG=2BE=2AE,∠BFG=75°=∠FBG,
∴FG=BG=2AE,
∵DF=2FM,FG=
| 2 |
∴DF=
| 2 |
| 2 |

点评:该题目考查了平行四边形的判定和性质,难点是由题意分析出作辅助线的方法,是比较复杂的题目.

练习册系列答案
相关题目
 某校针对某事件在本校学生中做了一次抽样调查,并把调查结果分为三种类型:
某校针对某事件在本校学生中做了一次抽样调查,并把调查结果分为三种类型: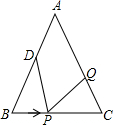 如图,已△ABC中,AB=AC=12厘米,BC=9厘,点D为AB的中点.
如图,已△ABC中,AB=AC=12厘米,BC=9厘,点D为AB的中点.