题目内容
7．
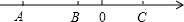如图，数轴上的三个点A、B、C分别表示有理数a、b、c，化简2|a-b|-|b+c|+|c-a|-|b-c|．
分析 根据数轴上点的位置判断出绝对值里边式子的正负，利用绝对值的代数意义化简即可得到结果．
解答 解：由数轴得：a＜b＜0＜c，且|b|＜|c|＜|a|，
∴a-b＜0，b+c＞0，c-a＞0，b-c＜0，
则原式=-2a+2b-b-c+c-a+b-c=-3a+2b-c．
点评 此题考查了整式的加减，数轴，以及绝对值，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．
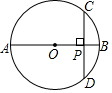⊙O的直径AB=10cm，弦CD⊥AB，垂足为P．若OP：OB=3：5，则CD的长为（ ）
⊙O的直径AB=10cm，弦CD⊥AB，垂足为P．若OP：OB=3：5，则CD的长为（ ）| A． | 6cm | B． | 4cm | C． | 8cm | D． | $\sqrt{91}$cm |
18．
如图，以原点O为圆心的圆交x轴于点A、B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB=25°，则∠OCD的度数是（ ）
如图，以原点O为圆心的圆交x轴于点A、B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB=25°，则∠OCD的度数是（ ）| A． | 45° | B． | 60° | C． | 65° | D． | 70° |
2．下列各式中，$\frac{3}{m}$，a-3，-2$\frac{1}{2}$，-$\frac{m}{3}$，2.7y3，π，$\frac{-2（x-y）}{5}$单项式的个数为（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
16．已知|a-3|+（b+4）2=0，那么（a+b）2003的值为（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2003 |