题目内容
18.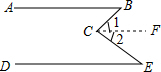 如图,AB∥DE,试证明∠B+∠E=∠BCE
如图,AB∥DE,试证明∠B+∠E=∠BCE证明:过点C作CF∥AB,
∵AB∥DE,AB∥CF,
∴DE∥CF
∴∠E=∠2
∵CF∥AB
∴∠B=∠1
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
分析 由AB∥DE,AB∥CF,根据平行于同一直线的两条直线平行,可证得DE∥CF,然后由两直线平行,内错角相等,证得∠E=∠2,∠B=∠1,继而证得结论.
解答 解:证明:过点C作CF∥AB,
∵AB∥DE,AB∥CF,
∴DE∥CF,
∴∠E=∠2,
∵CF∥AB
∴∠B=∠1,
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
故答案为:DE,CF,2,1.
点评 此题考查了平行线的性质.注意掌握两直线平行,内错角相等定理的应用是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列运算正确的是( )
| A. | 3a3+4a3=7a6 | B. | 3a2-4a2=-a2 | C. | 3a2•4a3=12a3 | D. | (3a3)2÷4a3=$\frac{3}{4}$a2 |
 顺达旅行社为吸引游客到黄山景区旅游,推出如下收费标准:
顺达旅行社为吸引游客到黄山景区旅游,推出如下收费标准: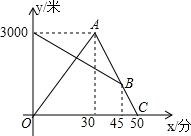 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,则下列说法:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,则下列说法: