题目内容
2.解不等式:3-$\frac{x-2}{2}$≤1+$\frac{x}{3}$.分析 根据不等式的解法解不等式.
解答 解:去分母得:18-3x+6≤6+2x,
移项合并同类项得:5x≥18,
系数化为1得:x≥$\frac{18}{5}$.
点评 本题考查了解简单不等式的能力,解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
相关题目
17.已知一元二次方程:2x2-3x-4=0的两个根分别是x1、x2,则x12x2+x1x22的值为( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
7.下列各式从左到右的变形正确的是( )
| A. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | B. | $\frac{0.2a+b}{a+0.2b}$=$\frac{2a+b}{a+2b}$ | ||
| C. | -$\frac{x+1}{x-y}$=$\frac{x-1}{x-y}$ | D. | $\frac{x-\frac{1}{2}y}{\frac{1}{2}x+y}$=$\frac{2x-y}{x+2y}$ |
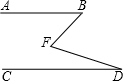 如图,已知AB∥CD,证明:∠BFD=∠B+∠D.(用两种方法证明)
如图,已知AB∥CD,证明:∠BFD=∠B+∠D.(用两种方法证明) 如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是AE=AC.
如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是AE=AC.