��Ŀ����
��ͼ���Ѻ���30��ǵ����ǰ�ABO����ƽ��ֱ������ϵ�У�A��B��������ֱ�Ϊ��3��0����(0��3 ��.����P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��
��.����P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1�� ��2 (���ȵ�λ/��)�qһֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ�� (���ȵ�λ/��)���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO-OB-BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
��2 (���ȵ�λ/��)�qһֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ�� (���ȵ�λ/��)���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO-OB-BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶��������������⣺
��С��1����A��B�����ֱ�߽���ʽ�� ��
��С��2����t��4ʱ����P������Ϊ �� ����t �� �� ����P���E�غϣ�
��С��3���� ����P����ֱ��EF�ĶԳƵ�P��. ���˶������У����γɵ��ı���PEP��FΪ���Σ���t��ֵ�Ƕ��٣�
�� ��t��2ʱ���Ƿ�����ŵ�Q��ʹ�á�FEQ �ס�BEP ?������, �����Q�����ꣻ�������ڣ���˵�����ɣ�

����1��
 ��������4��
��������4������2����0,
 ����
���� ������4�֣���2�֣�
������4�֣���2�֣���С��3���ٵ���
 ���߶�
���߶� ��ʱ����
��ʱ���� ��
�� ��
�� �ᣬ
�ᣬ Ϊ���㣨��ͼ1��
Ϊ���㣨��ͼ1��
��
 ,
, ,��
,�� ��
�� 90��
90�����
 �ա�
�ա� ����
���� �q
�q�֡�
 ,��
,�� 60��,��
60��,��
��
 ����
���� ,
,
��
 ��
��  ����������������1��
����������������1������P���߶�
 ��ʱ���γɵ��������Σ����������Σ�
��ʱ���γɵ��������Σ����������Σ�����P���߶�
 ��ʱ��
��ʱ����P��
 ��
�� ��
�� ��
�� ��
�� ��
�� �ֱ�Ϊ���㣨��ͼ2��
�ֱ�Ϊ���㣨��ͼ2��
��
 ,��
,�� ,��
,��
��
 �� �֡�
�� �֡�
��Rt��
 �У�
�У�
��
 �����
����� ����������������������������������������1��
����������������������������������������1���ڴ��کq�������£�

��
 ����
���� ,
, ��
��
����
 �Ƶ�
�Ƶ� ˳ʱ�뷽����ת90�㣬�õ�
˳ʱ�뷽����ת90�㣬�õ���
 ����ͼ3��
����ͼ3����
 ��
�� �����
����� ��ֱ��
��ֱ�� �ϣ�
�ϣ�C������Ϊ��
 ��
�� ��1��
��1����
 ��
�� ��
�� ����
���� �ڵ�Q,
�ڵ�Q,���
 �ס�
�ס�
��
 ���ɵ�Q������Ϊ����
���ɵ�Q������Ϊ���� ��
�� ��������������������1��
��������������������1�����ݶԳ��Կɵã�Q����ֱ��EF�ĶԳƵ�
 ����
���� ��
�� ��Ҳ��������������1�ֽ���:
��Ҳ��������������1�ֽ���:��1�������˴���ϵ������һ�κ�����
��2������Ҫ���յ�P���˶�·�ߣ�Ҫ���յ�P�ڲ�ͬ�ε��˶��ٶȣ�������ã�
��3���ٴ�����Ҫ�����������������P���߶�OA�ϣ����߶�OB�ϣ����߶�AB�ϣ��������ε��ж���֪�����߶�EF�Ĵ�ֱƽ��������x��Ľ��㣬�����һ��������P���߶�OB��ʱ���γɵ��������Σ����������Σ�����P���߶�BA��ʱ�����ݶԽ�����ƽ���һ��ഹֱ���ı�����������ã�
�ڵ�t��2ʱ������ĵ�P�����꣬����ȷ����BEP���������������ε��ж�����������õ�Q�����꣬����ʱҪע��𰸵IJ�Ψһ�ԣ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ��ͼ���Ѻ���30��ǵ����ǰ�ABO����ƽ��ֱ������ϵ�У�A��B��������ֱ�Ϊ��3��0���ͣ�0��3
��ͼ���Ѻ���30��ǵ����ǰ�ABO����ƽ��ֱ������ϵ�У�A��B��������ֱ�Ϊ��3��0���ͣ�0��3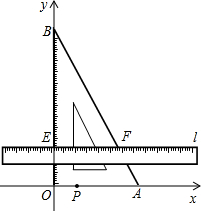 �Ķ����ϣ���ֱ���������У�30�����Ե�ֱ�DZ���б�ߵ�һ�룮
�Ķ����ϣ���ֱ���������У�30�����Ե�ֱ�DZ���б�ߵ�һ�룮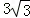 ��������P��A�㿪ʼ������AO��OB��BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��
��������P��A�㿪ʼ������AO��OB��BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��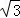 ��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ��
��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ�� 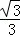 ����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO��OB��BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO��OB��BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
 ��.����P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��
��.����P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��