��Ŀ����
 ��ͼ���Ѻ���30��ǵ����ǰ�ABO����ƽ��ֱ������ϵ�У�A��B��������ֱ�Ϊ��3��0���ͣ�0��3
��ͼ���Ѻ���30��ǵ����ǰ�ABO����ƽ��ֱ������ϵ�У�A��B��������ֱ�Ϊ��3��0���ͣ�0��3| 3 |
| 3 |
| ||
| 3 |
�����������⣺
��1����A��B�����ֱ�߽���ʽ��
��2����t��4ʱ����P������Ϊ
��3��������P����ֱ��EF�ĶԳƵ�P�䣮���˶������У����γɵ��ı���PEP��FΪ���Σ���t��ֵ�Ƕ��٣�
�ڵ�t��2ʱ���Ƿ�����ŵ�Q��ʹ�á�FEQ�ס�BEP�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
��������1�������˴���ϵ������һ�κ�����
��2������Ҫ���յ�P���˶�·�ߣ�Ҫ���յ�P�ڲ�ͬ�ε��˶��ٶȣ�������ã�
��3���ٴ�����Ҫ�����������������P���߶�OA�ϣ����߶�OB�ϣ����߶�AB�ϣ��������ε��ж���֪�����߶�EF�Ĵ�ֱƽ��������x��Ľ��㣬�����һ��������P���߶�OB��ʱ���γɵ��������Σ����������Σ�����P���߶�BA��ʱ�����ݶԽ�����ƽ���һ��ഹֱ���ı�����������ã�
�ڵ�t��2ʱ������ĵ�P�����꣬����ȷ����BEP���������������ε��ж�����������õ�Q�����꣬����ʱҪע��𰸵IJ�Ψһ�ԣ�
��2������Ҫ���յ�P���˶�·�ߣ�Ҫ���յ�P�ڲ�ͬ�ε��˶��ٶȣ�������ã�
��3���ٴ�����Ҫ�����������������P���߶�OA�ϣ����߶�OB�ϣ����߶�AB�ϣ��������ε��ж���֪�����߶�EF�Ĵ�ֱƽ��������x��Ľ��㣬�����һ��������P���߶�OB��ʱ���γɵ��������Σ����������Σ�����P���߶�BA��ʱ�����ݶԽ�����ƽ���һ��ഹֱ���ı�����������ã�
�ڵ�t��2ʱ������ĵ�P�����꣬����ȷ����BEP���������������ε��ж�����������õ�Q�����꣬����ʱҪע��𰸵IJ�Ψһ�ԣ�
��� �⣺��1��y=-
�⣺��1��y=-
x+3
����4�֣�
��2����0��
����t=
����4�֣�����2�֣�
��3���ٵ���P���߶�AO��ʱ����F��FG��x�ᣬGΪ���㣨��ͼ1��
��OE=FG��EP=FP����EOP=��FGP=90��
���EOP�ա�FGP����OP=PG�q
�֡�OE=FG=
t����A=60�㣬��AG=
=
t
��AP=t��
��OP=3-t��PG=AP-AG=
t
��3-t=
t��t=
����1�֣�
����P���߶�OB��ʱ���γɵ��������Σ����������Σ�
����P���߶�BA��ʱ��
��P��PH��EF��PM��OB��H��M�ֱ�Ϊ���㣨��ͼ2��
��OE=
t����BE=3
-
t����EF=
=3-
��MP=EH=
EF=
���֡�BP=2��t-6��
��Rt��BMP�У�BP•cos60��=MP
��2��t-6��•
=
�����t=
����1�֣�
����������tΪ
��
ʱ���ı���PEP'FΪ���Σ�
�ڴ��کq�������£�
��t=2����OE=
��AP=2��OP=1
����BEP�Ƶ�E˳ʱ�뷽����ת90�㣬�õ� ��B'EC����ͼ3��
��B'EC����ͼ3��
��OB��EF��
���B'��ֱ��EF�ϣ�
��C����������ֵ����EO���ȣ�C�����������ֵ����EO-PO����
��C��������-
��
-1��
��F��FQ��B'C����EC�ڵ�Q��
���FEQ�ס�B'EC
��
=
=
=
���ɵ�Q������Ϊ��-
��
����1�֣�
���ݶԳ��Կɵã�Q����ֱ��EF�ĶԳƵ�Q'��-
��
��Ҳ������������1�֣�
 �⣺��1��y=-
�⣺��1��y=-| 3 |
| 3 |
��2����0��
| 3 |
| 9 |
| 2 |
��3���ٵ���P���߶�AO��ʱ����F��FG��x�ᣬGΪ���㣨��ͼ1��
��OE=FG��EP=FP����EOP=��FGP=90��
���EOP�ա�FGP����OP=PG�q
�֡�OE=FG=
| ||
| 3 |
| FG |
| tan60�� |
| 1 |
| 3 |
��AP=t��
��OP=3-t��PG=AP-AG=
| 2 |
| 3 |
��3-t=
| 2 |
| 3 |
| 9 |
| 5 |
����P���߶�OB��ʱ���γɵ��������Σ����������Σ�
����P���߶�BA��ʱ��

��P��PH��EF��PM��OB��H��M�ֱ�Ϊ���㣨��ͼ2��
��OE=
| ||
| 3 |
| 3 |
| ||
| 3 |
| BE |
| tan60�� |
| t |
| 3 |
��MP=EH=
| 1 |
| 2 |
| 9-t |
| 6 |
��Rt��BMP�У�BP•cos60��=MP
��2��t-6��•
| 1 |
| 2 |
| 9-t |
| 6 |
| 45 |
| 7 |
����������tΪ
| 9 |
| 5 |
| 45 |
| 7 |
�ڴ��کq�������£�
��t=2����OE=
| 2 |
| 3 |
| 3 |
����BEP�Ƶ�E˳ʱ�뷽����ת90�㣬�õ�
 ��B'EC����ͼ3��
��B'EC����ͼ3����OB��EF��
���B'��ֱ��EF�ϣ�
��C����������ֵ����EO���ȣ�C�����������ֵ����EO-PO����
��C��������-
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
��F��FQ��B'C����EC�ڵ�Q��
���FEQ�ס�B'EC
��
| BE |
| FE |
| B��E |
| FE |
| CE |
| QE |
| 3 |
| 2 |
| 3 |
| ||
| 3 |
���ݶԳ��Կɵã�Q����ֱ��EF�ĶԳƵ�Q'��-
| 2 |
| 3 |
| 3 |
���������⿼���˴���ϵ������һ�κ����Ľ���ʽ�������������ε��������ж��Լ����������ε��ж������ʣ�����Ĺؼ�Ҫע�����ν��˼���Ӧ�ã���Ҫע��𰸵IJ�Ψһ�ԣ�

��ϰ��ϵ�д�
 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
�����Ŀ
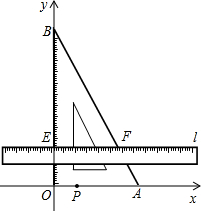 �Ķ����ϣ���ֱ���������У�30�����Ե�ֱ�DZ���б�ߵ�һ�룮
�Ķ����ϣ���ֱ���������У�30�����Ե�ֱ�DZ���б�ߵ�һ�룮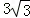 ��������P��A�㿪ʼ������AO��OB��BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��
��������P��A�㿪ʼ������AO��OB��BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��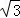 ��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ��
��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ�� 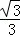 ����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO��OB��BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO��OB��BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
 ��.����P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��
��.����P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��
 ��.����P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��
��.����P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��