Question

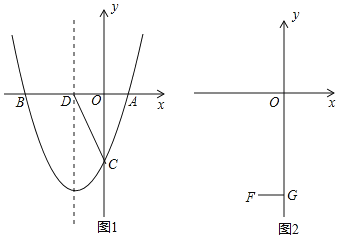
【题目】抛物线y＝x2＋bx＋c与x轴交于A(1，0)，B(m，0)，与y轴交于C.

（1）若m＝－3，求抛物线的解析式，并写出抛物线的对称轴；

（2）如图1，在(1)的条件下，设抛物线的对称轴交x轴于D，在抛物线对称轴左侧上有　一点E，使S△ACE＝S△ACD，求E点的坐标；

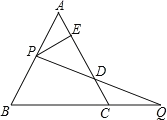
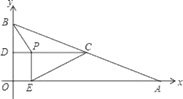
(3) 如图2，设F(－1，－4)，FG⊥y轴于G，在线段OG上是否存在点P，使 ∠OBP＝∠FPG?　若存在，求m的取值范围；若不存在，请说明理由．

Answer 1

【答案】（1）y=x2+2x-3；（2）点E坐标为（-2，-3）；（3）m的取值范围是：-4≤m≤4，且m≠0.

【解析】

(1)利用待定系数法求二次函数的解析式，并配方求对称轴；

(2)如图1，设E（n，n2+2n-3），先根据已知条件求S△ACE=3，根据不规则三角形面积等于铅直高度与水平宽度的积列式可求得n的值，并根据在对称轴左侧的抛物线上有一点E，则点E的横坐标小于-1，对n的值进行取舍，得到E的坐标；

(3) 设P(0，y)，根据相似三角形对应边成比例，列出相应的比例关系式，由y的取值范围判断m的取值范围，注意分两种情况讨论： ①当B在原点的左侧时，②当B在原点的右侧时.

（1）当m=-3,B(-3,0),

把A（1,0），B(-3,0)代入y＝x2＋bx＋c，联立方程组求得，b=2,c=-3,

抛物线的解析式为y=x2+2x-3，

对称轴x=-1；

（2）如图，设E(n，n2+2n-3)，由题意得：AD=1+1=2，OC=3，S△ACE=S△ACD=ADOC=3，

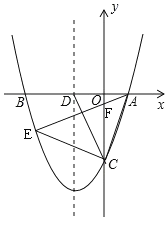
设直线AE的解析式为y=kx+b，把A(1，0)和E(n，n2+2n-3)代入，得

解得

∴直线AE的解析式为：y=(n+3)x-n-3，

∴F(0，-n-3).

∵C(0，-3)，

∴FC=-n-3-(-3)=-n，

∴S△ACE=FC(1-n)=3，

-n(1-n)=6，

n2-n-6=0，

∴n1=-2，n2=3(舍去)，

∴E(-2，-3).

(3)设点P（0，y）

①m＜0时，如图所示，

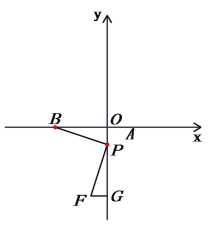
易证△POB～△FPG，得

∴

∴m=y2+4y=(y+2)2-4

∵-4＜y＜0，∴-4≤m＜0

②当m＞0时，如图所示，

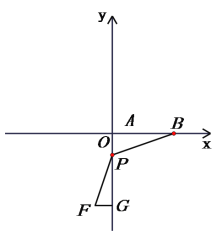
易证△POB～△FPG，得

∴

∴m= -y2 -4y= -(y+2)2+4

∵-4＜y＜0 ∴0＜m≤4

综上所述，m的取值范围是：-4≤m≤4，且m≠0.

故答案为：（1）y=x2+2x-3；（2）点E坐标为（-2，-3）；（3）m的取值范围是：-4≤m≤4，且m≠0.