Question

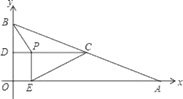
【题目】在平面直角坐标系中，已知点A、B的坐标分别为（10，0）、（0，4），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C以每秒1个单位匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线垂直时，点P运动的时间为_____秒．

Answer 1

【答案】1或4

【解析】

先求出CD和PE的长，再判定△EPC∽△PDB，列出相关的比例式，求得DP的长，根据点P的运动速度即可求得运动时间.

解：如图，当BP所在直线与EC所在直线垂直时，设BP与CE交于点F，

∵点A、B的坐标为(10，0)、(0，4)，

∴AO=10，BO=4，

∵CD⊥BO，C是AB的中点，

∴CD是△AOB的中位线，

∴BD=DO=BO=2=PE，CD=AO=5，CD∥AO，

设DP=x，则CP=5-x，

在Rt△PBD和Rt△PCF中，∠BPD=∠CPF，

∴PCE=∠DBP，

∴Rt△BPD∽Rt△CEP，

∴，

∴，

∴x=1或x=4，

∴当x=1时，即DP=1，运动时间为1秒；当x=4时，运动时间为4秒.

故答案为：1或4.