题目内容
 如图,在△ABC中,已知∠ABC=2∠BAC,BC=5,AC=9,则AB的长为
如图,在△ABC中,已知∠ABC=2∠BAC,BC=5,AC=9,则AB的长为考点:相似三角形的判定与性质
专题:
分析:作∠ABC的平分线,交AC与D,得出∠DBC=∠BAC,∠BDC=∠ABC,从而得出△ABC∽△BDC,通过三角形相似对应边成比例即可求得.
解答: 解:作∠ABC的平分线,交AC与D,
解:作∠ABC的平分线,交AC与D,
∵∠ABC=2∠BAC,
∴∠DBC=∠ABD=∠BAC,
∴AD=BD,∠BDC=2∠BAC=∠ABC,
∴△ABC∽△BDC,
∴DC:BC=BC:AC,
∴DC=
,
∴AD=BD=9-DC=9-
=
,
∵△ABC∽△BDC,
∴AB:BD=AC:CB
∴AB=
=
.
 解:作∠ABC的平分线,交AC与D,
解:作∠ABC的平分线,交AC与D,∵∠ABC=2∠BAC,
∴∠DBC=∠ABD=∠BAC,
∴AD=BD,∠BDC=2∠BAC=∠ABC,
∴△ABC∽△BDC,
∴DC:BC=BC:AC,
∴DC=
| 25 |
| 9 |
∴AD=BD=9-DC=9-
| 25 |
| 9 |
| 56 |
| 9 |
∵△ABC∽△BDC,
∴AB:BD=AC:CB
∴AB=
9×
| ||
| 5 |
| 56 |
| 5 |
点评:本题考查了相似三角形的判定和性质,作出辅助线构建相似三角形是本题的关键.

练习册系列答案
相关题目
以下二次根式:①
;②
;③
;④
中,与
是同类二次根式的是( )
| 12 |
| 22 |
|
| 27 |
| 3 |
| A、①和② | B、②和③ |
| C、①和④ | D、③和④ |
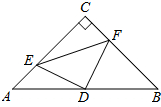 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论: