题目内容
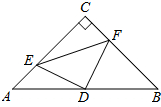 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C、E、D、F四点在同一个圆上,且该圆的面积最小为4π;
⑤DE•DF+CE•CF的值是定值为8.
其中正确结论的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:圆的综合题
专题:综合题
分析:连接CD,易得△ABC是等腰直角三角形,则∠A=∠B=45°,在根据等腰三角形的性质和直角三角形斜边上的中线性质得CD⊥AB,CD=AD=BD,则∠DCB=45°,得到∠A=∠DCF,然后利用“SAS”证明△ADE≌△CDF,得到ED=DF,∠CDF=∠ADE,易得∠EDC+∠CDF=90°,于是可判断△DFE是等腰直角三角形;当E、F分别为AC、BC中点时,易判断四边形CDFE是正方形;由△ADE≌△CDF得S△ADE=S△CDF,则S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ADC=
S△ABC═4,判断四边形CEDF的面积为定值;根据圆周角定理的推论得到点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,由△DEF是等腰直角三角形得到EF=
DE,再根据垂线段最短得到当DE⊥AC时,DE最短,此时DE=
AC=2,则EF的最小值为2
,根据圆的面积公式得到以EF为直径的圆的面积的最小值=2π;由S四边形CEDF=S△CFE+S△DEF=4,利用三角形面积公式得到
CE•CF+
DE•DF=4,所以DE•DF+CE•CF=8.
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:连接CD,如图1,
解:连接CD,如图1,
∵∠C=90°,AC=BC=4,
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∵D为AB的中点,
∴CD⊥AB,CD=AD=BD,
∴∠DCB=∠B=45°,
∴∠A=∠DCF,
在△ADE和△CDF中
∴△ADE≌△CDF(SAS),
∴ED=DF,∠CDF=∠ADE,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=90°,即∠EDF=90°,
∴△DFE是等腰直角三角形,所以①正确;
当E、F分别为AC、BC中点时,如图2,则AE=CE=CF=BF,DE=AE=CE,
∴CE=CF=DE=DF,
而∠ECF=90°,
∴四边形CDFE是正方形,所以②错误;
∵△ADE≌△CDF,
∴S△ADE=S△CDF,
∴S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ADC=
S△ABC=
×
×4×4=4,所以③错误;
 ∵△CEF和△DEF都为直角三角形,
∵△CEF和△DEF都为直角三角形,
∴点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,
∵△DEF是等腰直角三角形,
∴EF=
DE,
当DE⊥AC时,DE最短,此时DE=
AC=2,
∴EF的最小值为2
,
∴以EF为直径的圆的面积的最小值=π•(
•2
)2=2π,所以③错误;
∵S四边形CEDF=S△CFE+S△DEF=4,
∴
CE•CF+
DE•DF=4,
∴DE•DF+CE•CF=8,所以④正确.
故选B.
 解:连接CD,如图1,
解:连接CD,如图1,∵∠C=90°,AC=BC=4,
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∵D为AB的中点,
∴CD⊥AB,CD=AD=BD,
∴∠DCB=∠B=45°,
∴∠A=∠DCF,
在△ADE和△CDF中
|
∴△ADE≌△CDF(SAS),
∴ED=DF,∠CDF=∠ADE,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=90°,即∠EDF=90°,
∴△DFE是等腰直角三角形,所以①正确;
当E、F分别为AC、BC中点时,如图2,则AE=CE=CF=BF,DE=AE=CE,
∴CE=CF=DE=DF,
而∠ECF=90°,
∴四边形CDFE是正方形,所以②错误;
∵△ADE≌△CDF,
∴S△ADE=S△CDF,
∴S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 ∵△CEF和△DEF都为直角三角形,
∵△CEF和△DEF都为直角三角形,∴点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,
∵△DEF是等腰直角三角形,
∴EF=
| 2 |
当DE⊥AC时,DE最短,此时DE=
| 1 |
| 2 |
∴EF的最小值为2
| 2 |
∴以EF为直径的圆的面积的最小值=π•(
| 1 |
| 2 |
| 2 |
∵S四边形CEDF=S△CFE+S△DEF=4,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴DE•DF+CE•CF=8,所以④正确.
故选B.
点评:本题考查了圆的综合题:熟练掌握圆周角定理及其推论、等腰直角三角形的判定与性质、直角三角形斜边上的中线性质;会运用三角形全等证明线段和角相等.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
下列说法正确的是( )
| A、正数和负数统称为有理数 |
| B、互为相反数的两数之和为0 |
| C、零是最小的整数 |
| D、若两个数的绝对值相等,则这两个数必相等 |
广州亚运会期间,某纪念品原价168元,连续两次降价a%后售价为128元,下列所列方程正确的是( )
| A、168(1+a%)2=128 |
| B、168(1-a%)2=128 |
| C、168(1-2a%)=128 |
| D、168(1-a%)=128 |
下列说法不正确的是( )
| A、1的平方根是±1 | ||
| B、-1的立方根是-1 | ||
C、±
| ||
D、
|
在“科学与艺术”知识竞赛中,共有20道题,答对一道得10分,答错或不答的倒扣5分,若总分不少于80分,至少应答对多少道题( )
| A、10 | B、11 | C、12 | D、13 |
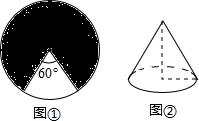 如图,小红同学在半径为4的圆中,剪去一个圆心角为60°的扇形,并将剩下部分(图中阴影部分)制成一个无缝隙且不重合的圆锥,则这个圆锥的高为
如图,小红同学在半径为4的圆中,剪去一个圆心角为60°的扇形,并将剩下部分(图中阴影部分)制成一个无缝隙且不重合的圆锥,则这个圆锥的高为 如图,在△ABC中,已知∠ABC=2∠BAC,BC=5,AC=9,则AB的长为
如图,在△ABC中,已知∠ABC=2∠BAC,BC=5,AC=9,则AB的长为