题目内容
17．
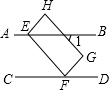如图，AB∥CD，将矩形EFGH的顶点E和F分别放在直线AB与CD上，若∠1=40°，则∠CFG的度数等于130°．
分析 延长HG交CD于M，由平行线的性质得出∠2=∠1=40°，与矩形的性质得出∠FGH=90°，求出∠FGM=90°，由三角形的外角性质即可得出∠CFG的度数．
解答 解：延长HG交CD于M，如图所示：
∵AB∥CD，
∴∠2=∠1=40°，
∵四边形EFGH是矩形，
∴∠FGH=90°，
∴∠FGM=90°，
∴∠CFG=∠FGM+∠2=90°+∠40°=130°；
故答案为：130°．
点评 本题考查了矩形的性质、平行线的性质以及三角形的外角性质；熟练掌握矩形的性质和平行线的性质是解决问题的关键．
练习册系列答案
相关题目
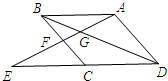如图，已知E为?ABCD的边DC延长线上的一点，且CE=CD，联结AE分别交BC、BD于点F、G．那么$\frac{DG}{BD}$=$\frac{2}{3}$．
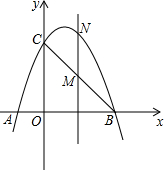如图，已知抛物线经过点A（-1，0），B（3，0），C（0，3）三点．
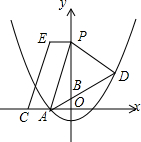在平面直角坐标系中，A（-2，0），B（0，1），C（-4，0）．点D（4，m）在直线AB上，抛物线y=$\frac{1}{4}$x2+bx+c恰好过A、D两点，点P（0，n）是抛物线对称轴上的一动点，将点P向左平移2个单位长度，对应点为E，连接PF、CE．
如图，在四边形ABCD中，∠A=90°，AD∥BC，E为AB的中点，连接CE，BD，过点E作FE⊥CE于点E，交AD于点F，连接CF，已知2AD=AB=BC．