题目内容
如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于点Q.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为 秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的
秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的 值;如果不能,说明理由.
值;如果不能,说明理由.
 |
(1)证明:如图,∵四边形ABCD是矩形,
∴AD∥BC,OD=OB,
∴∠PDO=∠QBO,
在△POD与△QOB中,
∠PDO=∠QBO
OD=OB
∠POD=∠QOB,
∴△POD≌△QOB(ASA), ∴OP=OQ,
∴四边形PBQD为平行四边形; (2)点P从点A出发运动t秒时, ,
, .
.
当四边形PBQD是菱形时, .
.
∵四边形ABCD是矩形,
∴∠BAP=90°,
∴在直角△ABP中,AB=3cm,
 , 即
, 即 ,
,
解得: ,
,
∴点P运动时间为 秒时,四边形PBQD能够成为菱形.
秒时,四边形PBQD能够成为菱形.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
不等式 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
|
| A. |
| B. |
| C. |
| D. |
|
下列说法正确的是( )
|
| A. | 近似数28.00与近似数28.0的精确度一样 |
|
| B. | 近似数0.32与近似数0.302的有效数字一样 |
|
| C. | 近似数2.4×102与240的精确度一样 |
|
| D. | 近似数220与近似数0.202都有三个有效数字 |
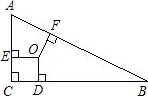
已知:如图,△ABC中,∠C=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10,BC=8,CA=6,则点O到三边AB、AC和BC的距离分别等于( )
|
| A. | 2、2、2 | B. | 3、3、3 | C. | 4、4、4 | D. | 2、3、5 |




 ”知识竞赛,在班里选取了若干名学生,分成人数相同的甲乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如下统计图。
”知识竞赛,在班里选取了若干名学生,分成人数相同的甲乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如下统计图。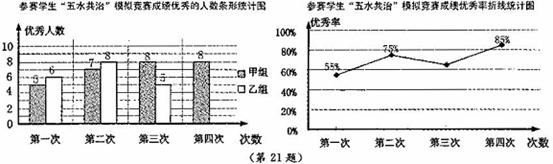
 根据统计图,解答下列问题:
根据统计图,解答下列问题: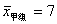 ,方差
,方差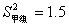 ,请通过计算说明,哪一组成绩优秀的人数较稳定?
,请通过计算说明,哪一组成绩优秀的人数较稳定? 的两个实根分别为
的两个实根分别为 、
、 ,那么
,那么 的值为 .
的值为 .

 .
.