题目内容
解方程：81（2x-5）2=144（x-3）2．
考点：解一元二次方程-因式分解法
专题：
分析：先移项，分解因式，即可得出两个一元一次方程，求出方程的解即可．
解答：解：81（2x-5）2=144（x-3）2．
移项得：81（2x-5）2-144（x-3）2=0，
[9（2x-5）+12（x-3）][9（2x-5）+12（x-3）]=0，
30x-81=0，6x-9=0，
x1=
，x2=
．
移项得：81（2x-5）2-144（x-3）2=0，
[9（2x-5）+12（x-3）][9（2x-5）+12（x-3）]=0，
30x-81=0，6x-9=0，
x1=
| 27 |
| 10 |
| 3 |
| 2 |
点评：本题考查了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，本题是根据因式分解法进行解答．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、三点确定一个圆 |
| B、正多边形既是轴对称图形也是中心对称图形 |
| C、等弧所对的圆周角相等 |
| D、垂直于半径的直线是圆的切线 |
方程x2-2x=0的解为（ ）
| A、x1=0，x2=2 |
| B、x1=0，x2=-2 |
| C、x1=x2=1 |
| D、x=2 |
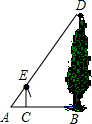如图，身高为1.6m的某同学想测量一棵大树的高度，她沿树影BA由B向A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m，CA=0.8m，求树高．