题目内容
 如图,在平面直角坐标系中,O是坐标原点,点A坐标为(2,0),点B坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC垂直于x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
如图,在平面直角坐标系中,O是坐标原点,点A坐标为(2,0),点B坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC垂直于x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.(1)当b=3时:①求直线AB相应的函数表达式;②当S△QOA=4时,求点P的坐标;
(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)①利用待定系数法求解即可,
②由①知点P坐标为(a,-
a+3),可求出点Q坐标,再利用S△QOA=
×|OA|×|-
a+3|求出a的值,即可得出点P的坐标.
(2)分两种情况①当∠QAC=90°且AQ=AC时,QA∥y轴,②,当∠AQC=90°且QA=QC时,过点Q作QH⊥x轴于点H,分别求解即可.
②由①知点P坐标为(a,-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(2)分两种情况①当∠QAC=90°且AQ=AC时,QA∥y轴,②,当∠AQC=90°且QA=QC时,过点Q作QH⊥x轴于点H,分别求解即可.
解答:解:(1)①设直线AB的函数表达式为:y=kx+b(k≠0),
将A(2,0),B(0,3)代入得
,解得
,
所以直线AB的函数表达式为y=-
x+3,
②由①知点P坐标为(a,-
a+3),
∴点Q坐标为(-a,-
a+3),
∴S△QOA=
×|OA|×|-
a+3|=
×2×|-
a+3|=|-
a+3|=-
a+3=4.
解得a=-
,
∴P点的坐标为(-
,4),
(2)设P点的坐标为(a,n),(a<0,n>0),
则点C,Q的坐标分别为C(a,0),Q(-a,n),
①如图1,当∠QAC=90°且AQ=AC时,QA∥y轴,
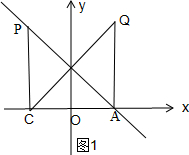
∴-a=2,
∴a=-2,
∴AC=4,从而AQ=AC=4,即|n|=4,由n>0得n=4,
∴P点坐标为(-2,4).
设直线AB的函数表达式为y=cx+b(c≠0),
将P(-2,4),A(2,0)代入得
,解得
,
∴a=-2,b=2.
②如图2,当∠AQC=90°且QA=QC时,过点Q作QH⊥x轴于点H,
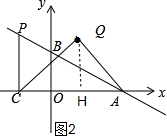
∴QH=CH=AH=
AC,
由Q(-a,n)知H(-a,0).
Q的横坐标-a=
,解得a=-
,
Q的纵坐标QH=
=
∴Q(
,
),
∴P(-
,
),
由P(-
,
),点A坐标为(2,0),可得直线AP的解析式为y=-
x+1,
∴b=1,
∴a=-
,b=1,
综上所述当△QAC是等腰直角三角形时,a=-2,b=2或a=-
,b=1.
将A(2,0),B(0,3)代入得
|
|
所以直线AB的函数表达式为y=-
| 3 |
| 2 |
②由①知点P坐标为(a,-
| 3 |
| 2 |
∴点Q坐标为(-a,-
| 3 |
| 2 |
∴S△QOA=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解得a=-
| 2 |
| 3 |
∴P点的坐标为(-
| 2 |
| 3 |
(2)设P点的坐标为(a,n),(a<0,n>0),
则点C,Q的坐标分别为C(a,0),Q(-a,n),
①如图1,当∠QAC=90°且AQ=AC时,QA∥y轴,

∴-a=2,
∴a=-2,
∴AC=4,从而AQ=AC=4,即|n|=4,由n>0得n=4,
∴P点坐标为(-2,4).
设直线AB的函数表达式为y=cx+b(c≠0),
将P(-2,4),A(2,0)代入得
|
|
∴a=-2,b=2.
②如图2,当∠AQC=90°且QA=QC时,过点Q作QH⊥x轴于点H,

∴QH=CH=AH=
| 1 |
| 2 |
由Q(-a,n)知H(-a,0).
Q的横坐标-a=
| a+2 |
| 2 |
| 2 |
| 3 |
Q的纵坐标QH=
| 2-a |
| 2 |
| 4 |
| 3 |
∴Q(
| 2 |
| 3 |
| 4 |
| 3 |
∴P(-
| 2 |
| 3 |
| 4 |
| 3 |
由P(-
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
∴b=1,
∴a=-
| 2 |
| 3 |
综上所述当△QAC是等腰直角三角形时,a=-2,b=2或a=-
| 2 |
| 3 |
点评:本题主要考查了一次函数综合题,涉及一次函数解析式,等腰直角三角形等知识,解题的关键是数形结合,分类讨论.

练习册系列答案
相关题目
心率即心脏在一定时间内跳动的次数,某次九年级体检对5名同学的心率测试结果如下(次/分):76,72,74,76,77.则下列说法错误的是( )
| A、这组测试结果的众数是76(次/分) |
| B、这组测试结果的中位数是74(次/分) |
| C、这组测试结果的平均数是75(次/分) |
| D、这组测试结果的方差是3.2(次/分)2 |
下列各组图形中,一定全等的是( )
| A、各有一个角是45°的两个等腰三角形 |
| B、两个等边三角形 |
| C、各有一个角是40°,腰长3cm的两个等腰三角形 |
| D、腰和顶角对应相等的两个等腰三角形 |