��Ŀ����
������11�֣���ͼ����������ABCD�У� AB=5��P��BC��������һ�㣬E��BC�ӳ�����һ�㣬����AP����PF��AP��ʹPF��PA������CF��AF��AF��CD���ڵ�G������PG��
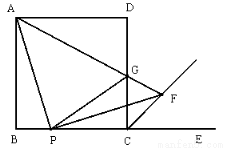
��1����֤����GCF����FCE��
��2���ж��߶�PG��PB��DG֮���������ϵ����֤����Ľ��ۣ�
��3����BP��2����ֱ��AB���Ƿ����һ��M��ʹ�ı���DMPF��ƽ���ı��Σ������ڣ����BM�ij��ȣ��������ڣ�˵�����ɣ�
��1��֤�������������2��PG��PB��DG�����������������3�����ڣ���BM=3��BM+AM=ABʱ���ı���DMPF��ƽ���ı��Σ�
��������
�����������1������F��FH��BE�ڵ�H�����������ε����ʣ�֤�á�BAP�ա�HPF�ó�PH��AB��BP��FH����һ���ó�BP��PC��PC��CH��CH��BP��FH����FHC��90����á�DCF��90-45��=45��ó����ۣ�
��2���ӳ�PB��K��ʹBK=DG������AK��֤�á�ABK�ա�ADG�͡�KAP�ա�GAP���ҳ�����ȵó����ۣ�
��3�������жϴ��ڣ���ֱ��AB��ȡһ��M��ʹ�ı���DMPF��ƽ���ı��Σ�֤�á�ABP�ա�DAM����һ����ý��ۼ���.
�����������1��֤��������F��FH��BE�ڵ�H��
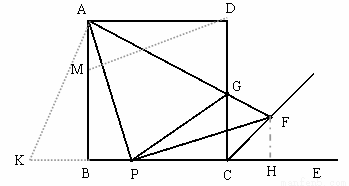
���ı���ABCD�������Σ����ABC����PHF����DCB��90,AB��BC��
���BAP����APB��90��
��AP��PF�����APB����FPH��90�����FPH����BAP ��
�֡�AP��PF�����BAP�ա�HPF��
��PH��AB��BP��FH��
��PH��BC��
��BP��PC��PC��CH��
��CH��BP��FH��
����FHC��90�����FCH����CFH��45��
���DCF��90��45��45��
���GCF����FCE��
��2��PG��PB��DG���������£�
�ӳ�PB��K��ʹBK=DG,
���ı���ABCD�������Σ���AB=AD, ��ABK��ADG=90��
���ABK�ա�ADG����AK=AG, ��KAB����GAD��
����APF=90 ��AP=PF�����PAF����PFA��45 ��
���BAP����KAB����KAP��45 ����PAF��
���KAP�ա�GAP��
��KP=PG,
��KB��BP=DG��BP��PG��
����PG��PB��DG��
��3�����ڣ�
��ͼ����ֱ��AB��ȡһ��M��ʹ�ı���DMPF��ƽ���ı��Σ�
��MD��PF����MD��FP��
�֡�PF=AP����MD=AP��
���ı���ABCD�������Σ���AB=AD����ABP=��DAM��
���ABP�ա�DAM����AM��BP=2��
��BM��AB��AM=5��2=3��
�൱BM=3��BM+AM=ABʱ���ı���DMPF��ƽ���ı��Σ�
���㣺�����ε����ʣ�ȫ�������ε��ж������ʣ�ƽ���ı��ε��ж�.
��������� ����1���ı��� �ı��Σ��ı��εij�����ѧ�п��е��ص�����֮һ����ֵһ��Ϊ10-14�֣�������ѡ����գ����֤�����ں����ۺ���Ŀ��Ϊ��������Ϊ�С���Ҫ�������ݣ��ٶ���ε��ڽǺͣ���Ǻ͵������ͼ�ε���Ƕ�����ƽ���ı��Σ����Σ����Σ������Σ��������ε����ʺ��ж���ͻ�Ʒ����������ն���Σ��ı��ε����ʺ��ж���������Ǹ��ʽ����ע�������ı��ε����ʽ����й��ı��ε�֤������ע�������Ŀ�Ľ�𣬶������������ ��������- ���ͣ�
- �Ѷȣ�
- ���ˣ�
- �꼶��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�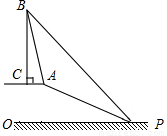
 �Ķ���
�Ķ��� �ֱ���
�ֱ��� ���
��� ���ϣ���
���ϣ��� ������Ϊ
������Ϊ ��˫����
��˫���� ��ͼ��
��ͼ�� ���е�
���е� ������
������ ���ڵ�
���ڵ� ������
������ ��
��
 ��ֵ����
��ֵ���� �����ꣻ
�����ꣻ �DZ�OC��һ�㣬�Ҧ�FCB�צ�DBE����ֱ��
�DZ�OC��һ�㣬�Ҧ�FCB�צ�DBE����ֱ�� �Ľ���ʽ.
�Ľ���ʽ. ��______________��
��______________��