题目内容
(10分)已知,如图,在笔山银子岩坡顶A处的同一水平面上有一座移动信号发射塔BC,笔山职中数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
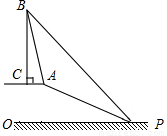
(1)坡顶A到地面PO的距离;(2)移动信号发射塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
(1)10米;(2)19米.
【解析】
试题分析:(1)先过点A作AH⊥PO,根据斜坡AP的坡度为1:2.4,得出 =
= ,设AH=5k,则PH=12k,AP=13k,求出k的值即可;
,设AH=5k,则PH=12k,AP=13k,求出k的值即可;
(2)先延长BC交PO于点D,根据BC⊥AC,AC∥PO,得出BD⊥PO,四边形AHDC是矩形,再根据∠BPD=45°,得出PD=BD,然后设BC=x,得出AC=DH=x﹣14,最后根据在Rt△ABC中,tan76°= ,列出方程,求出x的值即可.
,列出方程,求出x的值即可.
试题解析:【解析】
(1)过点A作AH⊥PO,垂足为点H,
∵斜坡AP的坡度为1:2.4,∴ =
= ,
,
设AH=5k,则PH=12k,由勾股定理,得AP=13k,
∴13k=26,解得k=2,
∴AH=10,
答:坡顶A到地面PQ的距离为10米.
(2)延长BC交PO于点D,
∵BC⊥AC,AC∥PO,∴BD⊥PO,
∴四边形AHDC是矩形,CD=AH=10,AC=DH,
∵∠BPD=45°,∴PD=BD,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°= ,即
,即 ≈4.01.
≈4.01.
解得x≈19.
答:移动信号发射塔BC的高度约为19米.

考点:解直角三角形的应用—仰角和俯角.
考点分析: 考点1:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案某林业部门要考查某种幼树在一定条件的移植成活率.在同样条件下,大量地对这种幼树进行移植,并统计成活情况,计算成活的频率.如下表:
移植总数(n) | 成活数(m) | 成活的频率 |
10 | 8 | 0.80 |
50 | 47 | 0.94 |
270 | 235 | 0.870 |
400 | 369 | 0.923 |
750 | 662 | 0.883 |
1500 | 1335 | 0.89 |
3500 | 3203 | 0.915 |
7000 | 6335 | 0.905 |
9000 | 8073 | 0.897 |
14000 | 12628 | 0.902 |
所以可以估计这种幼树移植成活的概率为( )
(A)0.1 (B)0.2 (C)0.8 (D)0.9




 B.
B.
 D.
D.
 ,y1),B(2,y2)为反比例函数
,y1),B(2,y2)为反比例函数 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP的长度之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP的长度之差达到最大时,点P的坐标是( )
 ,0) (B)(1,0) (C)(
,0) (B)(1,0) (C)( ,0) (D)(
,0) (D)( ,0)
,0)

 满足
满足 ,则
,则 的值是 .
的值是 .
 与⊙O的位置关系是( ).
与⊙O的位置关系是( ).