Question

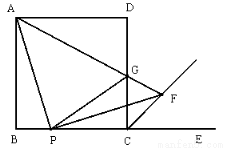
（本题6分）如图，矩形的顶点分别在轴和轴上，点的坐标为．双曲线的图像经过的中点，且与交于点，连接．

（1）求的值及点的坐标；

（2）若点是边OC上一点，且ΔFCB∽ΔDBE，求直线的解析式.

Answer 1

（1）；；（2）.

【解析】

试题分析：（1）根据B的坐标，以及四边形ABCO为矩形，确定出BC中点D的坐标，代入反比例解析式求出k的值；根据E在反比例图象上，且B与E横坐标相同，确定出E的坐标即可；

（2）由（1）得BD=1，BE=，BC=2，由△FBC∽△DEB，求出CF的长，继而确定OF的长，得到F的坐标，设直线FB的解析式为,将代入，求出与b的值，即可确定直线FB的解析式.

试题解析：【解析】
（1）在矩形OABC中，∵B点坐标为，∴边中点的坐标为（1,3），

又∵双曲线的图像经过点∴，∴；

∵点在上，∴点的横坐标为2．

又∵经过点, ∴点纵坐标为，

∴点纵坐标为.

（2）由（1）得，,

∵△FBC∽△DEB，∴，即，

∴，∴，即点的坐标为，

设直线的解析式为，而直线经过

∴，解得，

∴直线的解析式为.

考点：待定系数法求解析式；相似三角形的性质.

考点分析： 考点1：反比例函数 一般地，函数 （k是常数，k≠0）叫做反比例函数，自变量x的取值范围是x≠0的一切实数，函数值的取值范围也是一切非零实数。
注：
（1）因为分母不能为零，所以反比例函数函数的自变量x不能为零，同样y也不能为零；
（2）由，所以反比例函数可以写成的形式，自变量x的次数为-1；
（3）在反比例函数中，两个变量成反比例关系，即，因此判定两个变量是否成反比例关系，应看是否能写成反比例函数的形式，即两个变量的积是不是一个常数。

表达式：
x是自变量，y是因变量，y是x的函数
自变量的取值范围：
①在一般的情况下,自变量x的取值范围可以是不等于0的任意实数；
②函数y的取值范围也是任意非零实数。 反比例函数性质：
①反比例函数的表达式中，等号左边是函数值y，等号右边是关于自变量x的分式，分子是不为零的常数k，分母不能是多项式，只能是x的一次单项式；
②反比例函数表达式中，常数（也叫比例系数）k≠0是反比例函数定义的一个重要组成部分;
③反比例函数 （k是常数，k≠0）的自变量x的取值范围是不等式0的任意实数，函数值y的取值范围也是非零实数。 试题属性

• 题型：
• 难度：
• 考核：
• 年级：