题目内容
8.阅读以下文字并解决问题:对于形如x2+2ax+a2这样的二次三项式,我们可以直接用公式法把它分解成(x+a)2的形式,但对于二次三项式x2+6x-27,就不能直接用公式法分解了.此时,我们可以在x2+6x-27中间先加上一项9,使它与x2+6x的和构成一个完全平方式,然后再减去9,则整个多项式的值不变. 即:x2+6x-27=(x2+6x+9)-9-27=(x+3)2-62=(x+3+6)(x+3-6)=(x+9)(x-3),像这样,把一个二次三项式变成含有完全平方式的形式的方法,叫做配方法.(1)利用“配方法”因式分解:x2+4xy-5y2
(2)如果a2+2b2+c2-2ab-6b-4c+13=0,求a+b+c的值.
分析 (1)将前两项配方后即可得到(x+2y)2-(3y)2,然后利用平方差公式因式分解即可;
(2)由a2+2b2+c2-2ab-6b-4c+13=0,可得(a-b)2+(b-3)2+(c-2)2=0,求得a、b、c后即可得出答案.
解答 解:(1)x2+4xy-5y2
=(x2+4xy+4y2)-4y2-5y2
=(x+2y)2-(3y)2
=(x+2y+3y)(x+2y-3y)
=(x+5y)(x-y);
(2)∵a2+2b2+c2-2ab-6b-4c+13=0
∴(a2-2ab+b2)+(b2-6b+9)+(c2-4c+4)=0,
(a-b)2+(b-3)2+(c-2)2=0,
∴(a-b)2=0,(b-3)2=0,(c-2)2=0,
a=b=3,c=2,
∴a+b+c=8.
点评 考查了因式分解的知识,解题的关键是能够熟记完全平方公式及平方差公式的形式,并能正确的分组,难度不大.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
19.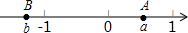 如图所示,数轴上A、B两点分别对应有理数a,b,则下列结论中正确的是( )
如图所示,数轴上A、B两点分别对应有理数a,b,则下列结论中正确的是( )
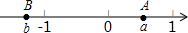 如图所示,数轴上A、B两点分别对应有理数a,b,则下列结论中正确的是( )
如图所示,数轴上A、B两点分别对应有理数a,b,则下列结论中正确的是( )| A. | a+b>0 | B. | ab>0 | C. | |a|-|b|>0 | D. | a-b>0 |
16. 如图所示,已知直线a∥b,c与a,b均相交,∠1=60°,则∠2为( )
如图所示,已知直线a∥b,c与a,b均相交,∠1=60°,则∠2为( )
 如图所示,已知直线a∥b,c与a,b均相交,∠1=60°,则∠2为( )
如图所示,已知直线a∥b,c与a,b均相交,∠1=60°,则∠2为( )| A. | 60° | B. | 70° | C. | 120° | D. | 150° |
20.下列几何体中,截面不可能是圆的是( )
| A. | 长方体 | B. | 圆锥 | C. | 球 | D. | 圆柱 |
18.下列各式成立的是( )
| A. | -80>0.8 | B. | -2.93<-2.94 | C. | -π>-3.14 | D. | $-\frac{3}{4}$<$-\frac{2}{3}$ |
 如图,线段AB=18cm,反向延长AB到C,使BC=2AC,D是AB上一点,且BD=$\frac{1}{6}$BC,若M为CD的中点,求AM的长.
如图,线段AB=18cm,反向延长AB到C,使BC=2AC,D是AB上一点,且BD=$\frac{1}{6}$BC,若M为CD的中点,求AM的长.