题目内容
8.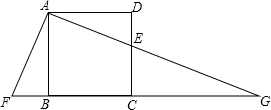 如图,E是正方形ABCD的边DC上的一点,过点A作AF⊥AE,交CB的延长线于点F,AE的延长线交BC的延长线于点G.若AF=13,DE=5,则CG的长是$\frac{84}{5}$.
如图,E是正方形ABCD的边DC上的一点,过点A作AF⊥AE,交CB的延长线于点F,AE的延长线交BC的延长线于点G.若AF=13,DE=5,则CG的长是$\frac{84}{5}$.
分析 首先利用余角的性质证明∠FAB=∠DAE,进而利用ASA即可证明△ABF≌△ADE,根据全等三角形的对应边相等的性质可得AE=AF,BF=DE,然后在直角△ABF中利用勾股定理求得AB的长,进而求出EC的长,再证明△ADE∽△GCE,根据相似三角形的对应边的比相等即可求解.
解答 解:正方形ABCD中,∠BAD=90°,AD=AB,
∵AF⊥AE,
∴∠FAB+∠BAE=90°
∵∠DAE+∠BAE=90°,
∴∠FAB=∠DAE,
在△ABF与△ADE中,
$\left\{\begin{array}{l}{∠FAB=∠DAE}\\{AB=AD}\\{∠EBA=∠D}\end{array}\right.$,
∴△ABF≌△ADE(ASA),
∴AE=AF,BF=DE,
∵∠FBA=90°,AF=7,BF=DE=2,
∴AB=$\sqrt{1{3}^{2}{-5}^{2}}$=12,
∴EC=DC-DE=7,
∵∠D=∠ECG=90°,∠DEA=∠CEG,
∴△ADE∽△GCE,
∴$\frac{AD}{CG}=\frac{DE}{CE}$,即$\frac{12}{CG}=\frac{5}{7}$,
∴CG=$\frac{84}{5}$.
故答案为:$\frac{84}{5}$.
点评 本题考查全等三角形的判定与性质以及相似三角形的判定与性质,勾股定理,正确证明△ABF≌△ADE,从而得到AF=AE,BF=DE是解题的关键.

练习册系列答案
相关题目
16.在平面直角坐标系中.点P(1,-2)关于y轴的对称点的坐标是( )
| A. | (1,2) | B. | (-1,-2) | C. | (-1,2) | D. | (-2,1) |
3.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元.
(不考虑除进价之外的其它费用)
(1)如果商店将购进的电视机与洗衣机销售完毕后获得利润为y元,购进电视机x台,求y与x的函数关系式(利润=售价-进价)
(2)请你帮助商店算一算有多少种进货方案?
(3)哪种进货方案待商店将购进的电视机与洗衣机销售完毕后获得利润最多?并求出最多利润.
| 类 别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
(不考虑除进价之外的其它费用)
(1)如果商店将购进的电视机与洗衣机销售完毕后获得利润为y元,购进电视机x台,求y与x的函数关系式(利润=售价-进价)
(2)请你帮助商店算一算有多少种进货方案?
(3)哪种进货方案待商店将购进的电视机与洗衣机销售完毕后获得利润最多?并求出最多利润.
13.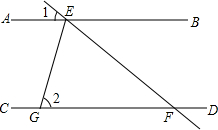 如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )
如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )
 如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )
如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )| A. | 68° | B. | 70° | C. | 71° | D. | 72° |
17.甲、乙两班学生参加植树造林,已知甲班每天比乙班少植3棵树,甲班植60棵树与乙班植80棵树所用天数相等.若设甲班每天植树x棵,则可列方程( )
| A. | $\frac{60}{x}=\frac{80}{x+3}$ | B. | $\frac{60}{x}=\frac{80}{x-3}$ | C. | $\frac{60}{x-3}=\frac{80}{x}$ | D. | $\frac{60}{x+3}=\frac{80}{x}$ |




 如图,直线y1=mx与直线y2=nx+8交于点P,P点坐标为(5.4),则不等式nx+8>mx的解为x<5.
如图,直线y1=mx与直线y2=nx+8交于点P,P点坐标为(5.4),则不等式nx+8>mx的解为x<5.