题目内容
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于
轴分别相交于![]() ,
,![]() 两点,与双曲线
两点,与双曲线![]() (
(![]() )相交于点
)相交于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,在点
,在点![]() 右侧的双曲线上取一点
右侧的双曲线上取一点![]() ,作
,作![]() 轴于
轴于![]() ,当以点
,当以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,则点
相似,则点![]() 的坐标是__________.
的坐标是__________.
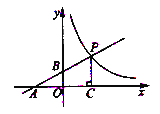
【答案】![]() 或
或![]()
【解析】
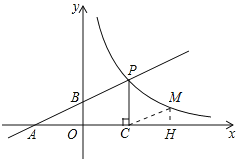
先求出点A、点B的坐标,设点M的坐标为(m,n),分两种情况:当△MCH∽△BAO和△MCH∽△ABO时,由相似得比例求出m的值,即可得出点M的坐标.
解:直线y=![]() x+1与x轴,y轴分别相交于A,B两点,
x+1与x轴,y轴分别相交于A,B两点,
令x=0得y=1,令y=0得x=-2,
∴A(-2,0),B(0,1).
设点M的坐标为(m,n),
∵点M在双曲线![]() 上,
上,
∴n=![]() .
.
当△MCH∽△BAO时,
可得![]() ,
,
即![]() ,
,
∴m-2=2n,即m-2=![]() ,
,
∴m2-2m-8=0,
解得:m1=4,m2=-2(舍去),
∴n=![]() =1,
=1,
∴M(4,1);
当△MCH∽△ABO时,
可得![]() ,
,
即![]()
整理得:2m-4=![]() ,
,
∴m2-2m-2=0,
解得:m1=1+![]() ,m2=1-
,m2=1-![]() (舍去),
(舍去),
∴n=![]() =
=![]() -2,
-2,
∴M(1+![]() ,
,![]() -2).
-2).
综上,M(4,1)或M(1+![]() ,
,![]() -2).
-2).
故答案为:(4,1)或(1+![]() ,
,![]() -2).
-2).

练习册系列答案
相关题目