题目内容
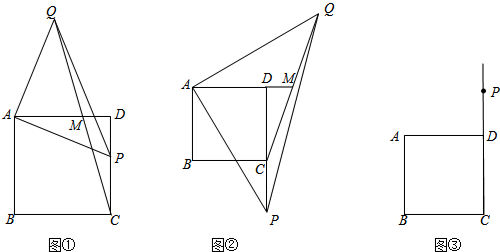
四边形ABCD为正方形(四边相等,四角为直角),点P为直线DC上一点,连接AP作等腰Rt△APQ,AP⊥AQ(其中A、P、Q按逆时针排列),直线CQ交直线AD于M点.
(1)如图①,点P在DC边上时,线段DM和CP之间是否存在某种确定的数量关系?写出你的结论并证明;
(2)如图②,点P在DC的延长线上时,其他条件不变,(1)中的结论是否仍然成立:证明你的结论;
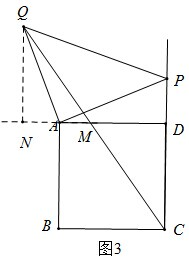
(3)如图③,点P在CD的延长线上时,其他条件不变,(1)中的结论是否仍然成立?请你完成图③,并直接写出你的结论,不需要证明.
(1)如图①,点P在DC边上时,线段DM和CP之间是否存在某种确定的数量关系?写出你的结论并证明;
(2)如图②,点P在DC的延长线上时,其他条件不变,(1)中的结论是否仍然成立:证明你的结论;
(3)如图③,点P在CD的延长线上时,其他条件不变,(1)中的结论是否仍然成立?请你完成图③,并直接写出你的结论,不需要证明.

考点:四边形综合题
专题:综合题
分析:(1)过点Q作QN⊥AD于点N,然后推出△ANQ≌△PDA,进而得到△QMN≌△CMD,最后通过等量代换得到结论;
(2)过点Q作QN⊥AD于点N,然后推理方法同(1);
(3)先根据题意把图补充完整,再写出和前面一样的结论,理由同前面两问.
(2)过点Q作QN⊥AD于点N,然后推理方法同(1);
(3)先根据题意把图补充完整,再写出和前面一样的结论,理由同前面两问.
解答:解:(1)DM=
CP,理由如下:
如图1所示,过点Q作QN⊥AD于点N,
因为△APQ是等腰直角三角形,
∴AQ=AP,
∵∠QAN+∠DAP=90°,∠APD+∠DAP=90°,
在△ANQ和△PDA中,
,
∴△ANQ≌△PDA,
∴AN=PD,QM=AD=CD,
∵AD=CD,
∴ND=CP,
在△QMN和△CMD中,
,
∴△QMN≌△CMD,
∴MN=MD,
∴DM=
ND=
CP;
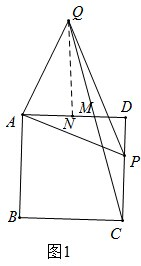
(2)(1)中的结论仍然成立,理由如下:
如图2所示,过点Q作QN⊥AD于点N,
∵∠QAN+∠NAP=90°,∠APD+∠NAP=90°,
∴∠QAN=∠APD,
在△ANQ和△PDA中,
,
∴△ANQ≌△PDA,
∴AN=PD,QN=AD=CD,
∵AD=CD,
∴ND=CP,
在△QMN和△CMD中,
,
∴△QMN≌△CMD,
∴MN=MD,
∴MD=
ND=
CP;
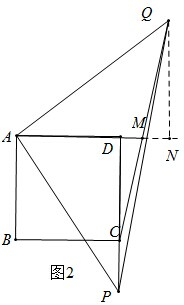
(3)(1)中的结论仍然成立,
如图3所示,MD=
CP.理由如下:
过点Q作QN⊥AD于点N,
∵∠NAQ+∠PAD=90°,∠APD+∠PAD=90°,
∴∠NAQ=∠APD,
在△ANQ和△PDA中,
,
∴△ANQ≌△PDA,
∴AN=PD,QN=AD=CD,
在△QMN和△CMD中,
,
∴△QMN≌△CMD,
∴MN=MD=
ND,
∵PD=AN,
∴MD=
(PD+CD)=
PC.
| 1 |
| 2 |
如图1所示,过点Q作QN⊥AD于点N,
因为△APQ是等腰直角三角形,
∴AQ=AP,
∵∠QAN+∠DAP=90°,∠APD+∠DAP=90°,
在△ANQ和△PDA中,
|
∴△ANQ≌△PDA,
∴AN=PD,QM=AD=CD,
∵AD=CD,
∴ND=CP,
在△QMN和△CMD中,
|
∴△QMN≌△CMD,
∴MN=MD,
∴DM=
| 1 |
| 2 |
| 1 |
| 2 |

(2)(1)中的结论仍然成立,理由如下:
如图2所示,过点Q作QN⊥AD于点N,
∵∠QAN+∠NAP=90°,∠APD+∠NAP=90°,
∴∠QAN=∠APD,
在△ANQ和△PDA中,
|
∴△ANQ≌△PDA,
∴AN=PD,QN=AD=CD,
∵AD=CD,
∴ND=CP,
在△QMN和△CMD中,
|
∴△QMN≌△CMD,
∴MN=MD,
∴MD=
| 1 |
| 2 |
| 1 |
| 2 |

(3)(1)中的结论仍然成立,
如图3所示,MD=
| 1 |
| 2 |
过点Q作QN⊥AD于点N,
∵∠NAQ+∠PAD=90°,∠APD+∠PAD=90°,
∴∠NAQ=∠APD,
在△ANQ和△PDA中,
|
∴△ANQ≌△PDA,
∴AN=PD,QN=AD=CD,
在△QMN和△CMD中,
|
∴△QMN≌△CMD,
∴MN=MD=
| 1 |
| 2 |
∵PD=AN,
∴MD=
| 1 |
| 2 |
| 1 |
| 2 |

点评:该题目考查了正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质,知识点比较多,关键是猜想出两个线段之间的数量关系,然后才能转化为寻求三角形全等来进行解决.

练习册系列答案
相关题目
 如图,△ABC中,∠C=90°,AC=40,BC=30.半径为(10+t)的圆的圆心P以2个单位/s的速度由点A出发,沿AC方向在射线AC上移动,设移动时间为t(单位:s).
如图,△ABC中,∠C=90°,AC=40,BC=30.半径为(10+t)的圆的圆心P以2个单位/s的速度由点A出发,沿AC方向在射线AC上移动,设移动时间为t(单位:s). 如图,把长AD=10cm,宽AB=8cm的矩形沿着AE对折,使点D落在BC边的F点上,求DE的长.
如图,把长AD=10cm,宽AB=8cm的矩形沿着AE对折,使点D落在BC边的F点上,求DE的长.