题目内容
已知AB弧和AC弧，是同圆的两段弧，且弧AB等于弧AC的2倍，则弦AB与弦AC之间的关系为（ ）
分析：取弧AB的中点D，连接AD，BD，则
=2
=2
，由已知条件
=2
，得出
=
=
，根据圆心角、弧、弦关系定理的推论得到AD=BD=AC，又在△ABD中，根据三角形三边关系定理得出AD+BD＞AB，即可得到AB＜2AC．
 |
| AB |
|
| AD |
|
| BD |
|
| AB |
|
| AC |
|
| AD |
|
| BD |
|
| AC |
解答：
解：如图，取弧AB的中点D，连接AD，BD，则
=2
=2
．
∵
=2
，
∴
=
=
，
∴AD=BD=AC．
在△ABD中，AD+BD＞AB，
∴AC+AC＞AB，即AB＜2AC．
故选B．
解：如图，取弧AB的中点D，连接AD，BD，则 |
| AB |
|
| AD |
|
| BD |
∵
|
| AB |
|
| AC |
∴
|
| AD |
|
| BD |
|
| AC |
∴AD=BD=AC．
在△ABD中，AD+BD＞AB，
∴AC+AC＞AB，即AB＜2AC．
故选B．
点评：本题主要考查了圆心角、弧、弦的关系及三角形三边关系定理，准确作出辅助线，得出AD=BD=AC是解题的关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
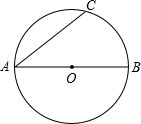已知AB、AC为⊙O的两条弦
是恒成立的．
恒成立，说明
恒成立；
恒成立，猜测：
（ ）也恒成立。
恒成立．
